Next: Triple integrals Up: MULTIPLE INTEGRATION Previous: Application of double integrals 索引
7.5
1.
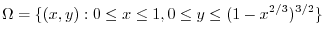
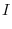 |
 |
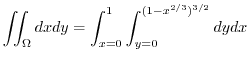 |
|
 |
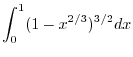 |
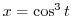 . Then
. Then
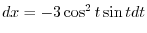
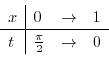
 |
 |
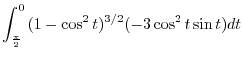 |
|
 |
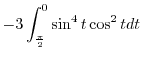 |
||
 |
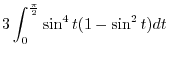 |
||
 |
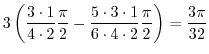 |
(b) We find the range of enclosure of
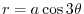 .To do so,we find the angle satisfying
.To do so,we find the angle satisfying 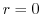 .
.
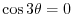 implies
implies
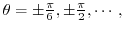 .Also,
.Also,
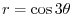 is symmetric about
is symmetric about 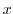 axis.Thus,the area we need to find is 12 times the area of region between
axis.Thus,the area we need to find is 12 times the area of region between
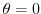 and
and
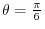 .Let
.Let 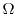 be the region between
be the region between
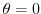 and
and
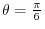 . Then using the polarcoordinates,
. Then using the polarcoordinates, 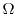 maps to
maps to
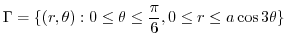
 |
 |
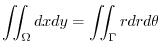 |
|
 |
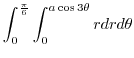 |
||
 |
![$\displaystyle \int_{0}^{\frac{\pi}{6}}\left[\frac{r^2}{2}\right]_{0}^{a\cos{\theta}} d\theta$](img851.png) |
||
 |
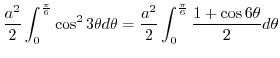 |
||
 |
![$\displaystyle \frac{a^2}{4}\left[\theta + \frac{\sin{6\theta}}{6}\right]_{0}^{\frac{\pi}{6}} = \frac{a^2}{4}(\frac{\pi}{6}) = \frac{a^2 \pi}{24}$](img853.png) |
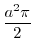 .
.
First, we find the points of intersection.,
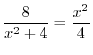
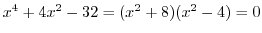 .Then
.Then 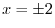 .Thus we express
.Thus we express 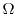 using V-simple.
using V-simple.
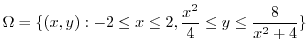
 |
 |
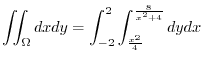 |
|
 |
![$\displaystyle \int_{-2}^{2}\left[y\right]_{\frac{x^2}{4}}^{\frac{8}{x^2 + 4}} dx$](img860.png) |
||
 |
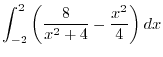 |
||
 |
![$\displaystyle \left[8\cdot\frac{1}{2}\tan^{-1}{\frac{x}{2}} - \frac{x^3}{12}\right]_{-2}^{2}$](img862.png) |
||
 |
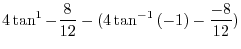 |
||
 |
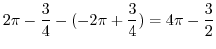 |
2.
(a) To find the area of a surface,we need a function
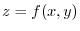 and the
and the 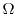 which is created by the orthogonal projection of
which is created by the orthogonal projection of
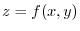 .
Note that
.
Note that
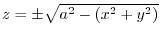 .Now take an orthogona projection of the curve. Then
.Now take an orthogona projection of the curve. Then 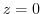 and
and
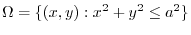
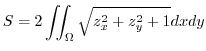
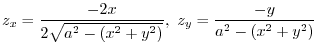
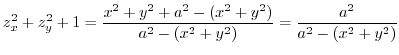
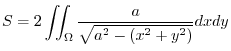
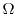 is a circle. Using the polarcoordinates, we have
is a circle. Using the polarcoordinates, we have
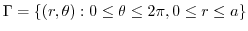
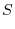 |
 |
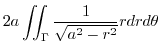 |
|
 |
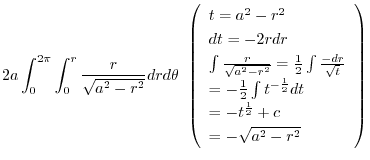 |
||
 |
![$\displaystyle 2a \int_{0}^{2\pi}\left[-\sqrt{a^2 - r^2}\right]_{0}^{r} d\theta$](img876.png) |
||
 |
![$\displaystyle 2a \int_{0}^{2\pi}a d\theta = 2a^2 \left[\theta\right]_{0}^{2\pi}$](img877.png) |
||
 |
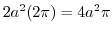 |
(b) To find the area of a surface,we need a function of the surface
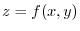 and the
and the  which is created by the orthogonal projection of
which is created by the orthogonal projection of
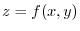 .
We use the orthogonal projection of
.
We use the orthogonal projection of
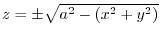 .
.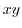 . In other words, we let
. In other words, we let 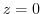 . Then
. Then
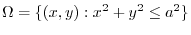
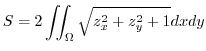
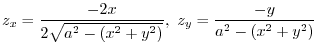
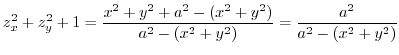
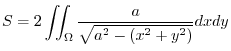
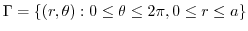
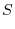 |
 |
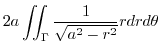 |
|
 |
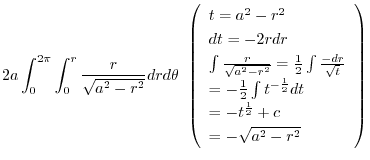 |
||
 |
![$\displaystyle 2a \int_{0}^{2\pi}\left[-\sqrt{a^2 - r^2}\right]_{0}^{r} d\theta$](img876.png) |
||
 |
![$\displaystyle 2a \int_{0}^{2\pi}a d\theta = 2a^2 \left[\theta\right]_{0}^{2\pi}$](img877.png) |
||
 |
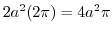 |
(c) To find the area of a surface,we need a function of the surface
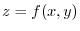 and the
and the 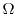 which is created by the orthogonal projection of
which is created by the orthogonal projection of
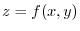 ..
In this problem, we cut the surface by
..
In this problem, we cut the surface by
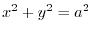 . Then we take orthogonal projection. Then,
. Then we take orthogonal projection. Then,
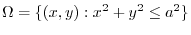
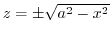 implies
implies
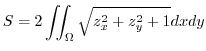
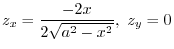
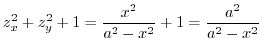
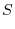 |
 |
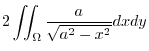 |
|
 |
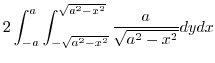 |
||
 |
![$\displaystyle 2\int_{-a}^{a}\left[\frac{ay}{\sqrt{a^2 - x^2}}\right]_{-\sqrt{a^2 - x^2}}^{\sqrt{a^2 - x^2}} dx$](img885.png) |
||
 |
![$\displaystyle 4\int_{-a}^{a}a dx = 8a\int_{0}^{a} dx = 8a[x]_{0}^{a} = 8a^2$](img886.png) |
(d) The surface area 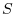 of revolving solid rotating
of revolving solid rotating
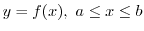 around
around 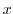 axis is given by
axis is given by
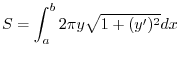
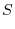 |
 |
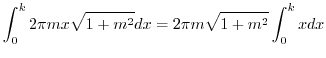 |
|
 |
![$\displaystyle 2\pi m \sqrt{1 + m^2}[x]_{0}^{k} = \pi m \sqrt{1 + m^2} k^2$](img891.png) |
3. Given the continuos function
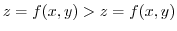 on
on 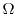 , Then the volume of the solid bounded by the sufaces
, Then the volume of the solid bounded by the sufaces 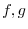 and the suface parallel to the
and the suface parallel to the 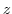 axis is given by
axis is given by
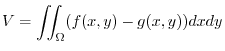
(a)
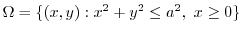 . Using the polarcoordinates,
. Using the polarcoordinates,
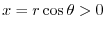 implies that
implies that  maps to
maps to
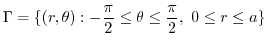
 |
 |
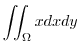 |
|
 |
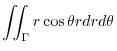 |
||
 |
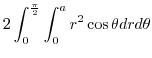 |
||
 |
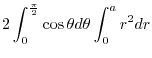 |
||
 |
![$\displaystyle 2\left[\sin{\theta}\right]_{0}^{\frac{\pi}{2}}\left[\frac{r^3}{3}\right]_{0}^{a}$](img904.png) |
||
 |
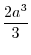 |
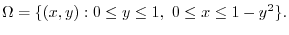
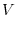 |
 |
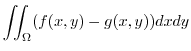 |
|
 |
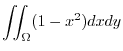 |
||
 |
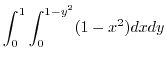 |
||
 |
![$\displaystyle \int_{0}^{1}\left[x - \frac{x^3}{3}\right]_{0}^{1 - y^2} dy$](img911.png) |
||
 |
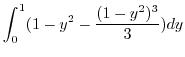 |
||
 |
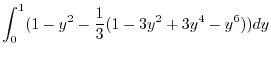 |
||
 |
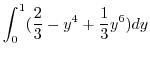 |
||
 |
![$\displaystyle \left[\frac{2}{3}y - \frac{y^5}{5} + \frac{1}{21}y^7\right]_{0}^{1}$](img915.png) |
||
 |
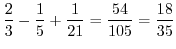 |
(c)
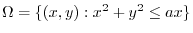 .Using the polarcoordinte, we express the boundary of
.Using the polarcoordinte, we express the boundary of 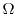 . Then
. Then
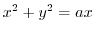 implies
implies
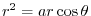 .Thus,
.Thus,
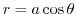 becomes 0 at,
becomes 0 at,
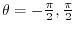 .Thus,
.Thus,
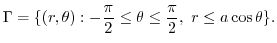
 |
 |
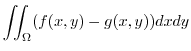 |
|
 |
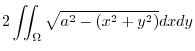 |
||
 |
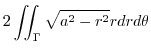 |
||
 |
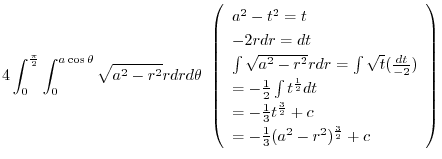 |
||
 |
![$\displaystyle 4\int_{0}^{\frac{\pi}{2}}\left[-\frac{1}{3}(a^2 - r^2)^{\frac{3}{2}}\right]_{0}^{a\cos{\theta}} d\theta$](img926.png) |
||
 |
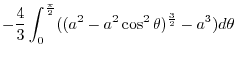 |
||
 |
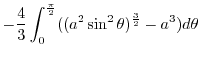 |
||
 |
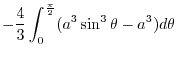 |
||
 |
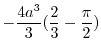 |
(d) The line of intersection of the cone
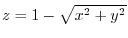 and the plane
and the plane 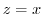 is
is
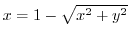 .Then the volume of the solid is given by the group of straight lines that pass through the boundary of
.Then the volume of the solid is given by the group of straight lines that pass through the boundary of
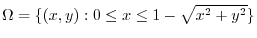 and are parallel to the
and are parallel to the 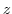 axis.Using the polarcoordintate, we express the boundary of
axis.Using the polarcoordintate, we express the boundary of 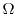 . Then
. Then
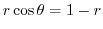 implies
implies
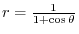 .
.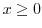 implies
implies
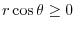 .Thus,
.Thus,
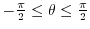 .Thus,,
.Thus,,
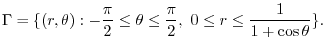
 |
 |
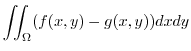 |
|
 |
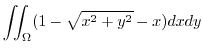 |
||
 |
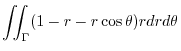 |
||
 |
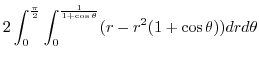 |
||
 |
![$\displaystyle 2\int_{0}^{\frac{\pi}{2}}\left[\frac{r^2}{2} - \frac{r^3}{3}(1 + \cos{\theta})\right]_{0}^{\frac{1}{1 + \cos{\theta}}} d\theta$](img943.png) |
||
 |
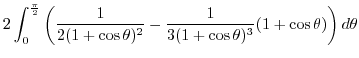 |
||
 |
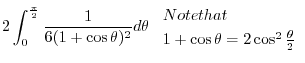 |
||
 |
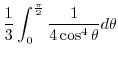 |
||
 |
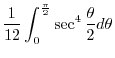 |
||
 |
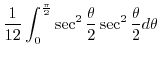 |
||
 |
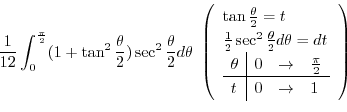 |
||
 |
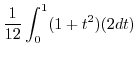 |
||
 |
![$\displaystyle \frac{1}{6}\left[t + \frac{t^3}{3}\right]_{0}^{1}$](img951.png) |
||
 |
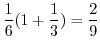 |