- 1.
- Find the area of the following regionsüD
- (a)
- The region enclosed by the curve
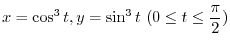 and
and 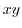 axes.
axes.
- (b)
- The region enclosed by
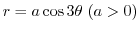 .
.
- (c)
- The region enclosed by
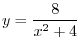 and
and
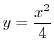 .
.
- 2.
- Find the surface area of the following region.üD
- (a)
- A sphere
 with the radius
with the radius 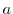 .
.
- (b)
- The region
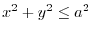 corresponds to
corresponds to 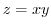 .
.
- (c)
- The region common to the cylinders
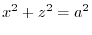 and
and
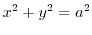 .
.
- (d)
- The surface created by evolving
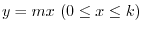 with
with 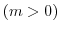 around
around 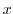 axis.
axis.
- 3.
- Find the volume of the following solids.
- (a)
- The cylinder
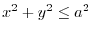 with
with
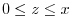 .
.
- (b)
- The closed region
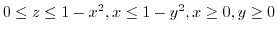 .
.
- (c)
- The sphere
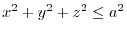 common to
common to
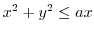 .
.
- (d)
- The region enclosed by the conical surface
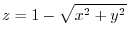 and the planes
and the planes 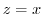 and
and 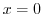 .
.
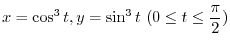 and
and 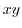 axes.
axes.
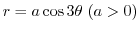 .
.
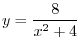 and
and
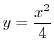 .
.
 with the radius
with the radius 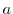 .
.
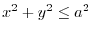 corresponds to
corresponds to 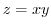 .
.
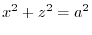 and
and
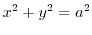 .
.
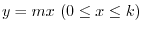 with
with 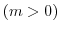 around
around 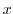 axis.
axis.
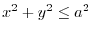 with
with
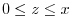 .
.
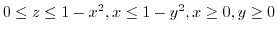 .
.
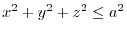 common to
common to
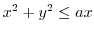 .
.
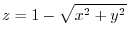 and the planes
and the planes 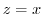 and
and 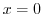 .
.