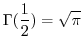next up previous index
Next: Application of double integrals Up: MULTIPLE INTEGRATION Previous: Improper integrals   索引

7.4 Answer

7.4

1.

(a) Using H-simple,

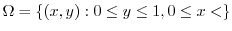
$\displaystyle \Omega = \{(x,y) : 0 \leq y \leq 1, 0 \leq x < \}$

Thus,

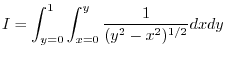
$\displaystyle I = \int_{y=0}^{1}\int_{x=0}^{y}\frac{1}{(y^2 - x^2)^{1/2}}dx dy$

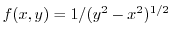Note that， $f(x,y) = 1/(y^2 - x^2)^{1/2}$ is not defined at 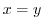$x = y$. Thus we let

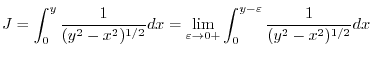
$\displaystyle J = \int_{0}^{y} \frac{1}{(y^2 - x^2)^{1/2}}dx = \lim_{\varepsilon \to 0+}\int_{0}^{y-\varepsilon}\frac{1}{(y^2 - x^2)^{1/2}}dx$

Then
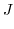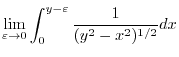$\displaystyle J$ $\displaystyle =$ $\displaystyle \lim_{\varepsilon \to 0}\int_{0}^{y-\varepsilon}\frac{1}{(y^2 - x^2)^{1/2}}dx$  
  $\displaystyle =$ $\displaystyle \lim_{\varepsilon \to 0}[\sin^{-1}{x}{y}]_{0}^{y - \varepsilon} = \frac{\pi}{2}$  

Therefore，

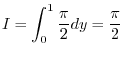
$\displaystyle I = \int_{0}^{1}\frac{\pi}{2}dy = \frac{\pi}{2}$

(b) 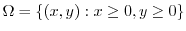$\Omega = \{(x,y) : x \geq 0, y \geq 0\}$ is not bounded. Thus we consider

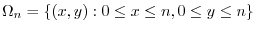
$\displaystyle \Omega_{n} = \{(x,y) : 0 \leq x \leq n, 0 \leq y \leq n\}$

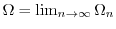Then since $\Omega = \lim_{n \to \infty}\Omega_{n}$, we have
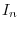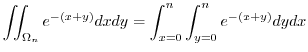$\displaystyle I_{n}$ $\displaystyle =$ $\displaystyle \iint_{\Omega_{n}}e^{-(x+y)}dxdy = \int_{x=0}^{n}\int_{y=0}^{n}e^{-(x+y)}dy dx$  
  $\displaystyle =$ $\displaystyle \int_{0}^{n}\left[-e^{-(x+y)}\right]_{0}^{n} \ dx$  
  $\displaystyle =$ $\displaystyle \int_{0}^{n}(-e^{(x+n)} + e^{-x})dx = \left[e^{-(x+n)} + e^{-x}\right]_{0}^{n}$  
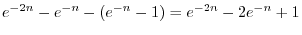  $\displaystyle =$ $\displaystyle e^{-2n} - e^{-n} - (e^{-n} - 1) = e^{-2n} - 2e^{-n} + 1$  

Therefore,

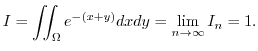
$\displaystyle I = \iint_{\Omega}e^{-(x+y)}dxdy = \lim_{n \to \infty}I_{n} = 1.$

(c)

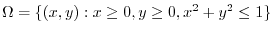$\Omega = \{(x,y) : x \geq 0, y \geq 0, x^2 + y^2 \leq 1\}$ is bounded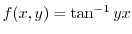． $f(x,y) = \tan^{-1}{y}{x}$ is bounded on 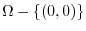$\Omega - \{(0,0)\}$．Thus we consider

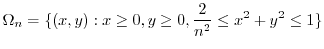
$\displaystyle \Omega_{n} = \{(x,y) : x \geq 0, y \geq 0, \frac{2}{n^2} \leq x^2 + y^2 \leq 1\}$

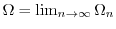Since $\Omega = \lim_{n \to \infty}\Omega_{n}$,

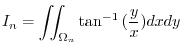
$\displaystyle I_{n} = \iint_{\Omega_{n}}\tan^{-1}{(\frac{y}{x})}dxdy$

Now using the polarcoordinates,

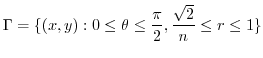
$\displaystyle \Gamma = \{(x,y) : 0 \leq \theta \leq \frac{\pi}{2}, \frac{\sqrt{2}}{n} \leq r \leq 1\}$

Thus,
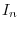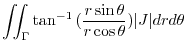$\displaystyle I_{n}$ $\displaystyle =$ $\displaystyle \iint_{\Gamma}\tan^{-1}{(\frac{r\sin{\theta}}{r\cos{\theta}})}\vert J\vert drd\theta$  
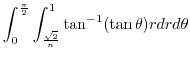  $\displaystyle =$ $\displaystyle \int_{0}^{\frac{\pi}{2}}\int_{\frac{\sqrt{2}}{n}}^{1}\tan^{-1}(\tan{\theta})r dr d\theta$  
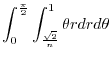  $\displaystyle =$ $\displaystyle \int_{0}^{\frac{\pi}{2}}\int_{\frac{\sqrt{2}}{n}}^{1}\theta r dr d\theta$  
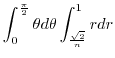  $\displaystyle =$ $\displaystyle \int_{0}^{\frac{\pi}{2}} \theta d\theta \int_{\frac{\sqrt{2}}{n}}^{1}r dr$  
  $\displaystyle =$ $\displaystyle \left[\frac{\theta^2}{2}\right]_{0}^{\frac{\pi}{2}}\left[\frac{r^... ...\right]_{\frac{\sqrt{2}}{n}}^{1} = \frac{\pi^2}{8}(\frac{1}{2} - \frac{1}{n^2})$  

Therefore,

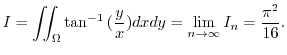
$\displaystyle I = \iint_{\Omega}\tan^{-1}{(\frac{y}{x})}dxdy = \lim_{n \to \infty}I_{n} = \frac{\pi^2}{16}.$

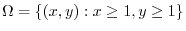(d) $\Omega = \{(x,y) : x \geq 1, y \geq 1\}$ is not bounded. Thus we consider

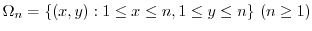
$\displaystyle \Omega_{n} = \{(x,y) : 1 \leq x \leq n, 1 \leq y \leq n\} \ (n \geq 1)$

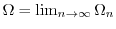Then since $\Omega = \lim_{n \to \infty}\Omega_{n}$, we have
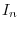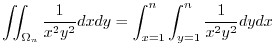$\displaystyle I_{n}$ $\displaystyle =$ $\displaystyle \iint_{\Omega_{n}}\frac{1}{x^2 y^2}dxdy = \int_{x=1}^{n}\int_{y=1}^{n}\frac{1}{x^2 y^2}dy dx$  
  $\displaystyle =$ $\displaystyle \int_{1}^{n}\left[-\frac{1}{x^2 y}\right]_{1}^{n} \ dx$  
  $\displaystyle =$ $\displaystyle \int_{1}^{n}(\frac{1}{x^2} - \frac{1}{x^2 n})dx = \left[-\frac{1}{x} + \frac{1}{xn}\right]_{1}^{n}$  
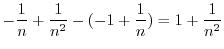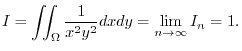
  $\displaystyle =$ $\displaystyle -\frac{1}{n} + \frac{1}{n^2} - (-1 + \frac{1}{n}) = 1 + \frac{1}{n^2}$  

Therefore,

$\displaystyle I = \iint_{\Omega}\frac{1}{x^2 y^2}dxdy = \lim_{n \to \infty}I_{n} = 1.$

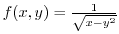(e) $f(x,y) = \frac{1}{\sqrt{x - y^2}}$ is not defined on the curve 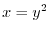$x = y^2$．Then we let 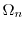$\Omega_{n}$ be the set of 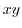$xy$ plane except 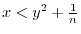$x < y^2 + \frac{1}{n}$．Now using H-simple, we hae

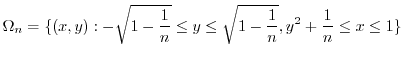
$\displaystyle \Omega_{n} = \{(x,y) : -\sqrt{1 - \frac{1}{n}} \leq y \leq \sqrt{1 - \frac{1}{n}}, y^2 + \frac{1}{n} \leq x \leq 1\}$

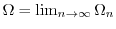Since $\Omega = \lim_{n \to \infty}\Omega_{n}$,
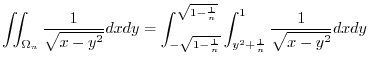$\displaystyle I_{n}$ $\displaystyle =$ $\displaystyle \iint_{\Omega_{n}}\frac{1}{\sqrt{x - y^2}}dxdy = \int_{-\sqrt{1 -... ...sqrt{1 - \frac{1}{n}}}\int_{y^2 + \frac{1}{n}}^{1}\frac{1}{\sqrt{x - y^2}}dx dy$  
  $\displaystyle =$ $\displaystyle \int_{-\sqrt{1 - \frac{1}{n}}}^{\sqrt{1 - \frac{1}{n}}}\left[2\sqrt{x - y^2}\right]_{y^2 + \frac{1}{n}}^{1} \ dy$  
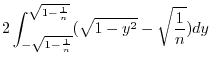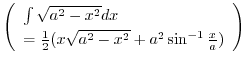  $\displaystyle =$ $\displaystyle 2\int_{-\sqrt{1 - \frac{1}{n}}}^{\sqrt{1 - \frac{1}{n}}}(\sqrt{1 - y^2} - \sqrt{\frac{1}{n}})dy \ $   ere$\displaystyle \left(\begin{array}{l} \int{\sqrt{a^2 - x^2}}dx\\ = \frac{1}{2}(x\sqrt{a^2 - x^2} + a^2 \sin^{-1}{\frac{x}{a}}) \end{array}\right)$  
  $\displaystyle =$ $\displaystyle 2(\frac{1}{2}) \left[\sqrt{1 - y^2} + \sin^{-1}{y} - \sqrt{\frac{1}{n}} y\right]_{-\sqrt{1 - \frac{1}{n}}}^{\sqrt{1 - \frac{1}{n}}}$  
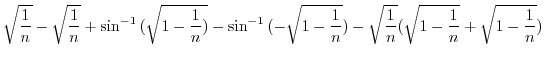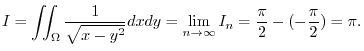
  $\displaystyle =$ $\displaystyle \sqrt{\frac{1}{n}} - \sqrt{\frac{1}{n}} + \sin^{-1}{(\sqrt{1 - \f... ...{1}{n}})} - \sqrt{\frac{1}{n}}(\sqrt{1 - \frac{1}{n}} + \sqrt{1 - \frac{1}{n}})$  

Thereore,

$\displaystyle I = \iint_{\Omega}\frac{1}{\sqrt{x - y^2}}dxdy = \lim_{n \to \infty}I_{n} = \frac{\pi}{2} - (-\frac{\pi}{2}) = \pi.$

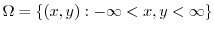(f) $\Omega = \{(x,y) : -\infty < x, y < \infty\}$ is not bouned. Then we consier

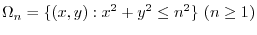
$\displaystyle \Omega_{n} = \{(x,y) : x^2 + y^2 \leq n^2\} \ (n \geq 1)$

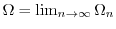Then $\Omega = \lim_{n \to \infty}\Omega_{n}$．Using the polarcoordinates,

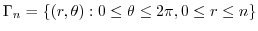
$\displaystyle \Gamma_{n} = \{(r,\theta) : 0 \leq \theta \leq 2\pi, 0 \leq r \leq n\}$

Thus
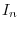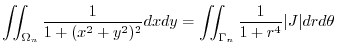$\displaystyle I_{n}$ $\displaystyle =$ $\displaystyle \iint_{\Omega_{n}}\frac{1}{1 + (x^2 + y^2)^2}dxdy = \iint_{\Gamma_{n}}\frac{1}{1 + r^4}\vert J\vert dr d\theta$  
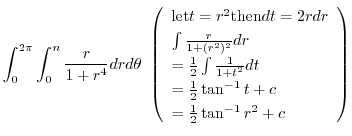  $\displaystyle =$ $\displaystyle \int_{0}^{2\pi}\int_{0}^{n}\frac{r}{1 + r^4}dr d\theta \ \left(\b... ...rac{1}{2}\tan^{-1}{t} + c\\ = \frac{1}{2}\tan^{-1}{r^2} + c \end{array}\right)$  
  $\displaystyle =$ $\displaystyle \int_{0}^{2\pi} d\theta\left[\frac{1}{2}\tan^{-1}{r^2}\right]_{0}^{2\pi}$  
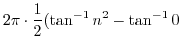  $\displaystyle =$ $\displaystyle 2\pi \cdot \frac{1}{2}(\tan^{-1}n^2 - \tan^{-1}{0}$  

Therefore,

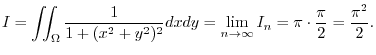
$\displaystyle I = \iint_{\Omega}\frac{1}{1 + (x^2 + y^2)^2}dxdy = \lim_{n \to \infty}I_{n} = \pi \cdot \frac{\pi}{2} = \frac{\pi^2}{2}.$

2.

Let $\displaystyle{t = x^{\frac{1}{2}}}$. Then $\displaystyle{2tdt = dx}$．Thus,

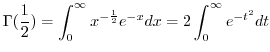
$\displaystyle \Gamma(\frac{1}{2}) = \int_{0}^{\infty} x^{-\frac{1}{2}}e^{-x} dx = 2\int_{0}^{\infty} e^{-t^2} dt $

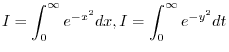Let $\displaystyle{I = \int_{0}^{\infty} e^{-x^2} dx, I = \int_{0}^{\infty} e^{-y^2} dt}$. Then

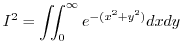
$\displaystyle I^2 = \iint_{0}^{\infty} e^{-(x^2 + y^2)} dx dy $

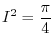Note that $\displaystyle{I^2 = \frac{\pi}{4}}$ implies $\displaystyle{\Gamma(\frac{1}{2}) = \sqrt{\pi}}$

next up previous index
Next: Application of double integrals Up: MULTIPLE INTEGRATION Previous: Improper integrals   索引