Next: 6.9 Answer Up: PARTIAL DIFFERENTIATION Previous: 6.8 Answer Ź§ł°
|
Exercise
|
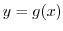 derived from the following functionüD
derived from the following functionüD
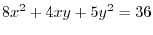
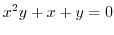
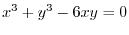
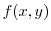 under the following condition
under the following condition
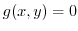 .
.
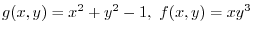
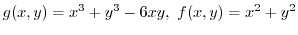
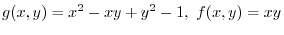
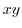 when the point
when the point
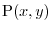 moves on the straight line
moves on the straight line
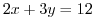 üD
üD
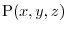 moves over the sphere
moves over the sphere
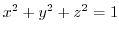 , Find the maximum and minimum values of
, Find the maximum and minimum values of
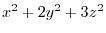 .
.