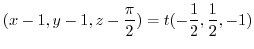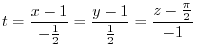Next: Extremum with side conditions Up: PARTIAL DIFFERENTIATION Previous: Implicit functions 索引
6.8
1.
(a)
Let
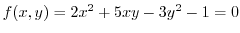 . Then find the total differential of
. Then find the total differential of 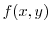 .
.
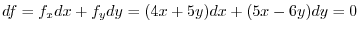
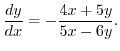
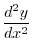 |
 |
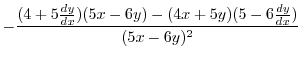 |
|
 |
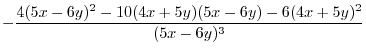 |
Let
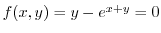 . Then find the total differential of
. Then find the total differential of 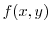 .
.
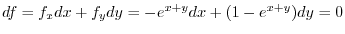
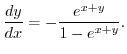
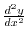 . Here we use
. Here we use
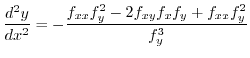
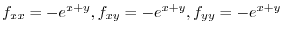
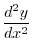 |
 |
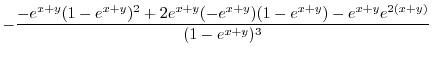 |
|
 |
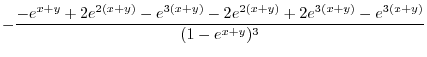 |
||
 |
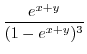 |
Let
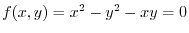 . Then find the total differntial of
. Then find the total differntial of 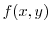 .
.
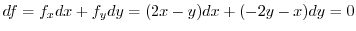
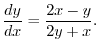
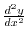 . We use
. We use
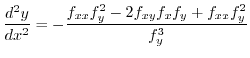
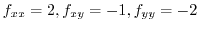
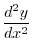 |
 |
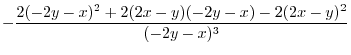 |
|
 |
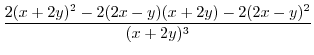 |
Let
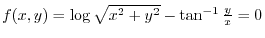 , Then find the total differential of
, Then find the total differential of 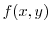 .
.
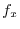 |
 |
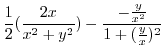 |
|
 |
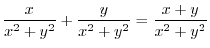 |
||
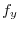 |
 |
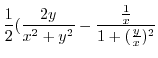 |
|
 |
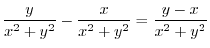 |
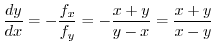
Next we find
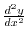 .
.
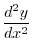 |
 |
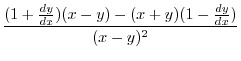 |
|
 |
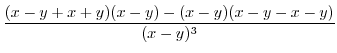 |
||
 |
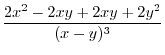 |
||
 |
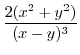 |
2.
(a)
Let
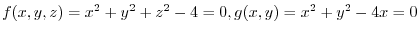 . Then find the total differential
. Then find the total differential 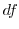 .
.
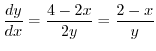
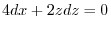
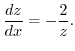
(b)
Let
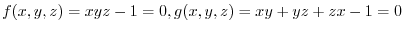 . Then find the total differential.
. Then find the total differential.
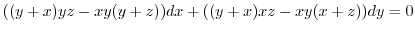
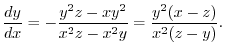
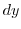 . Then
. Then
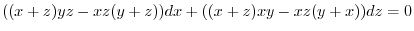
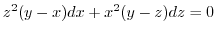
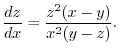
3.
From the equation
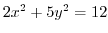 , we find
, we find
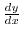 . Then
. Then
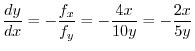
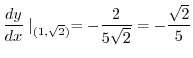
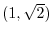 is
is
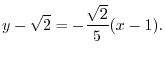
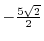 .Thus the equation of the normal line goew through
.Thus the equation of the normal line goew through
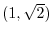 is
is
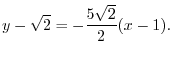
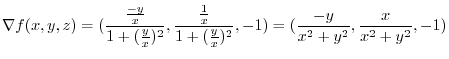
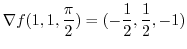
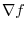 is orthogonal to the surface
is orthogonal to the surface
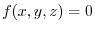 . Now take any point
. Now take any point 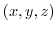 on the tangent plane
on the tangent plane 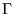 . Then the vectors
. Then the vectors
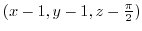 and
and
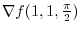 are orthogonal.Thus, the equation of the tangent plane is
are orthogonal.Thus, the equation of the tangent plane is
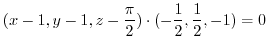
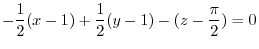
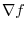 . Thus for any point
. Thus for any point 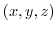 on the normal line, we have,
on the normal line, we have,