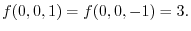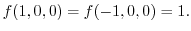Next: MULTIPLE INTEGRATION Up: PARTIAL DIFFERENTIATION Previous: Extremum with side conditions 索引
6.9
1.
Suppose that implicit function 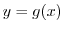 determined by
determined by
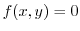 attains the extremum
attains the extremum
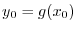 at
at 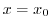 . Then
. Then
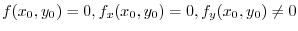
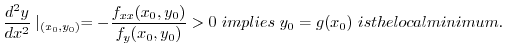
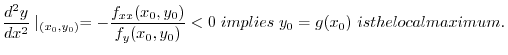
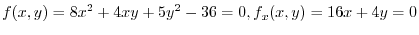
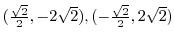 .
Next ,
.
Next ,
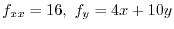
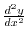 .
.
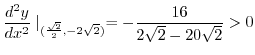
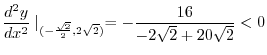
Thus for
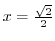 ,
,
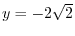 is the local minimum and for
is the local minimum and for
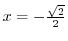 ,
,
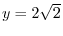 is the local maximum.
is the local maximum.
First we find 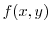 so that
so that
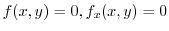 .
.
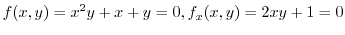
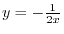 .Put this into
.Put this into
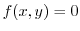 . Then
. Then
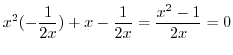
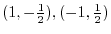 .
Next,
.
Next,
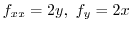
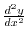 .
.
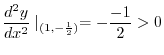
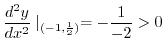
Thus for 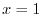 ,
,
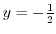 is the local minimum and for
is the local minimum and for 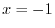 ,
,
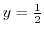 is also the local minimum.
is also the local minimum.
First we find 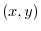 so that
so that
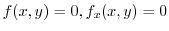 .
.
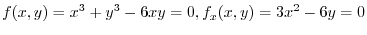
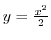 .Put this inot
.Put this inot
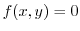 . Then
. Then
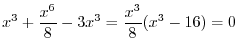
![$(0,0), (2\sqrt[3]{2}, 2\cdot2^{\frac{2}{3}})$](img466.png) .
Next,
.
Next,
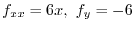
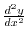 .
.
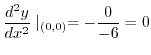
![$\displaystyle \frac{d^2 y}{dx^2}\mid_{(2\sqrt[3]{2}, 2\cdot2^{\frac{2}{3}})} = -\frac{6\cdot 2\sqrt[3]{2}}{-6} > 0$](img469.png)
Thus for
![$x = 2\sqrt[3]{2}$](img470.png) ,
,
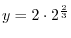 is the local minimum.
is the local minimum.
2. Suppose that at least one of
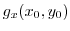 or
or
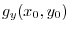 is not 0.
is not 0.
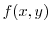 attains the extremun at
attains the extremun at
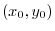 under the condition
under the condition
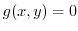 if
if
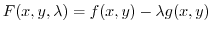
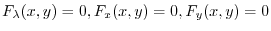
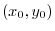 .
Here, the points satisfying
.
Here, the points satisfying
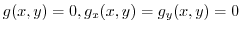 are called singular points.
are called singular points.
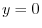 , the equation (1.9) implies,
, the equation (1.9) implies,
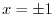 and the equation (1.10) implies
and the equation (1.10) implies
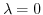 .
For
.
For 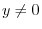 ,the equation (1.11) implies
,the equation (1.11) implies
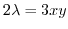 .Now put this into the equation (1.10). Then
.Now put this into the equation (1.10). Then
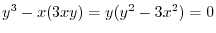 implies
implies
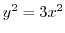 .Now put this into the equation (1.9). Then
.Now put this into the equation (1.9). Then
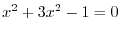 implies
implies
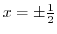 .Thus,
.Thus,
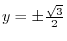 .Therefore the solution to the equations (1.9),(1.10),(1.11) are
.Therefore the solution to the equations (1.9),(1.10),(1.11) are
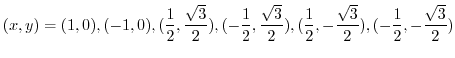
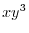 is
is
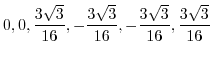
 is bounded closed region and
is bounded closed region and  is continuous on this region. Thus it takes the maximum and the minimum. Thus, the maximum value is
is continuous on this region. Thus it takes the maximum and the minimum. Thus, the maximum value is
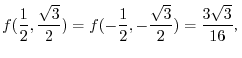
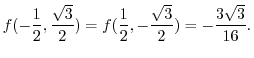
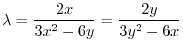
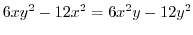
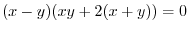
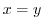 or
or
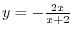 .
.
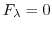 implies
implies
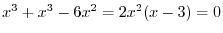 .Therefore
.Therefore
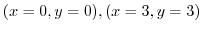 .
On the other hand, The part of
.
On the other hand, The part of
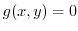 in the 1st quadrant with the origin is the bounded closed curve and
in the 1st quadrant with the origin is the bounded closed curve and 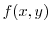 is continuous on the curve. Thus, it takes the maximum and the minimum. Therefore, the maximimun value is
is continuous on the curve. Thus, it takes the maximum and the minimum. Therefore, the maximimun value is
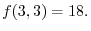
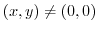 , then
, then
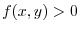 . Thus
. Thus
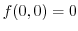 is the local minimum and also the minimum.
is the local minimum and also the minimum.
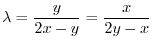
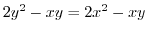
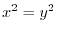
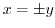 .
.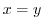 ,
,
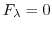 implies
implies
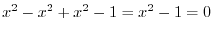 .Thus,
.Thus,
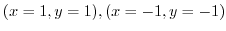 .
.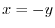 のとき
のとき
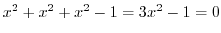 .Therefore,
.Therefore,
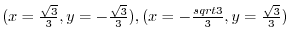 .
Then,The value of
.
Then,The value of
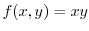 is,
is,
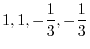
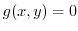 is bounded closed region and
is bounded closed region and  is continuous on this region. Thus,
is continuous on this region. Thus,  takes the maximum and the minimum. The maximum value is
takes the maximum and the minimum. The maximum value is
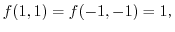
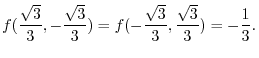
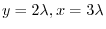 .Put this into the equation (1.18). Then
.Put this into the equation (1.18). Then
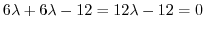
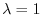 and
and
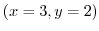 .On the other hand,
.On the other hand,
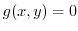 is bounded closed region and
is bounded closed region and 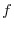 is continuous on this region. Thus,
is continuous on this region. Thus, 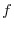 attains the maximum and minimum.
attains the maximum and minimum.
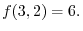
4.
Let
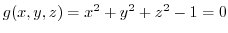 .
.
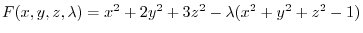 .
.
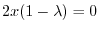 ,
,
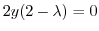 ,
,
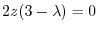 .Here,for
.Here,for 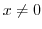 ,
,
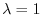 implies
implies 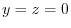 .Put this into (1.21).
.Put this into (1.21).
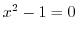 implies
implies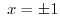
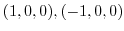 .For
.For 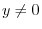 ,
,
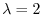 implies
implies 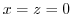 .Put this into the equation (1.21).
.Put this into the equation (1.21).
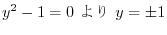
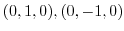 .For
.For 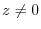 ,
,
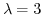 implies
implies 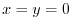 .Put this intp the equation (1.21). Then
.Put this intp the equation (1.21). Then
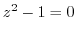 implies
implies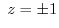
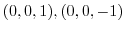 .From this, we fin the value of the equation (1.21).
.From this, we fin the value of the equation (1.21).
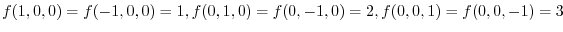
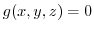 is bounded closed region and
is bounded closed region and 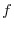 is continuous on this region. Thus,
is continuous on this region. Thus, 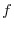 attains the maximum and minimum.
The maximun value is
attains the maximum and minimum.
The maximun value is