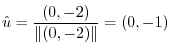Next: Differentiation of composite functions Up: PARTIAL DIFFERENTIATION Previous: Gradient and directional derivatives 索引
6.5
1. The directional derivative is given by
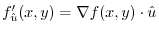
 is the directional unit vector in the direction of
is the directional unit vector in the direction of  .
.
(a)
Find a unit directional vector 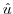 . Then
. Then
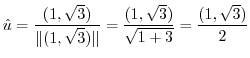
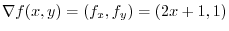
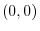 is
is
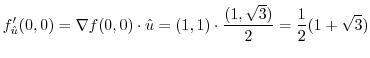
Find the unit vector 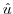 . Then
. Then
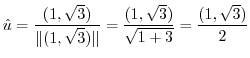
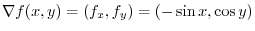
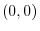 is
is
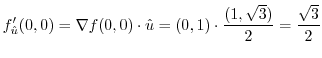
2.
(a)
We fin the unit directional vector 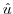 . Then
. Then
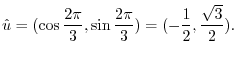
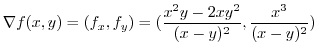
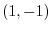 is
is
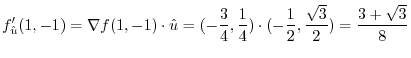
(b)
We find the unit directional vector 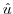 . Then
. Then
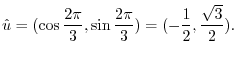
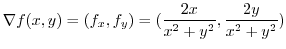
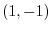 is
is
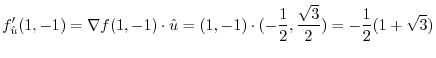
3.
(a)
We find the unit directional vector 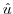 . Then
. Then
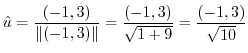
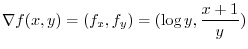
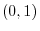 .
.
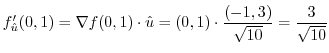
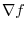 . Thus,
. Thus,
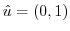
(b)
We find the unit directional vector 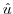 . Then
. Then
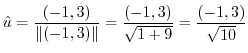
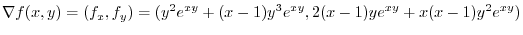
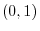 . Thus
. Thus
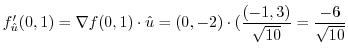
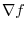 .
.