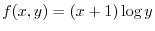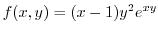Gradient and directional derivatives

Exercise

1.

Find the directional derivative of the following functions at $(0,0)$ in the direction of $(1, \sqrt{3})$．

(a)

$${f(x,y) = x^2 + x + y}$$

(b)

$${f(x,y) = \cos{x} + \sin{y}}$$

2.

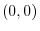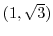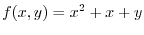
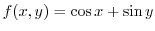
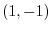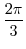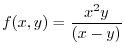
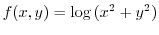
Find the directional derivative of the following functions at $(1,-1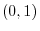)$ in the direction of $${\frac{2 \pi}{3}}$$．

(a)

$${f(x,y) = \frac{x^2 y}{(x - y)}}$$

(b)

$${f(x,y) = \log{(x^2 + y^2)}}$$

3.

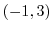Find the directional derivative of the following functions at $(0,1)$ in the direction of $(-1,3)$．Find the directional unit vector so that the directional derivatives becomes the maximum.

(a)

$${f(x,y) = (x+1)\log{y}}$$

(b)

$${f(x,y) = (x-1)y^{2}e^{xy}}$$