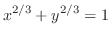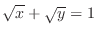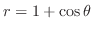- 1.
- Find the area of the figure surrounded by the following curvesD
- (a)
-
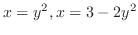
- (b)
-
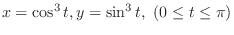 and
and  -axis
-axis
- 2.
- Find the volume of a rotating body formed by rotating the following plane figure around the
 axis
axis
- (a)
-
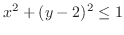
- (b)
-
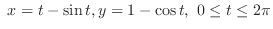 and
and  -axisD
-axisD
- 3.
- Find the length of the following curvesD
- (a)
-
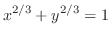
- (b)
-
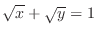
- (c)
-
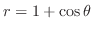
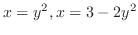
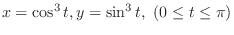 and
and  -axis
-axis
 axis
axis
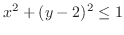
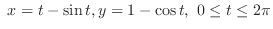 and
and  -axisD
-axisD