Next: この文書について... Up: INTEGRATION Previous: Applications of definite integral
3.10
1.
(a)
Find the intersection of 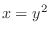 and
and
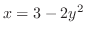 . Then
. Then
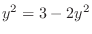 implies
implies 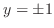 . Thus these two curves intersects at
. Thus these two curves intersects at 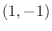 and
and 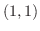 .Now think of this figure's are as a sum of
.Now think of this figure's are as a sum of 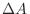 .Cut this figure by the line perpendicular to
.Cut this figure by the line perpendicular to 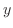 -axis. Then the width is given by the right-hand curve
-axis. Then the width is given by the right-hand curve 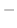 the left-hand curve. The hight is given by the
the left-hand curve. The hight is given by the 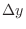 . Thus,
. Thus,
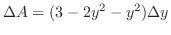
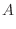 |
 |
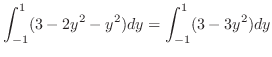 |
|
 |
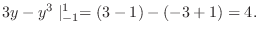 |
This figure is not differentiable at
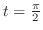 . So, we integrate from
. So, we integrate from 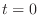 to
to
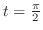 and double the value.Cut the figure by the rectangle with small width. Then the area of the rectangle is given by
and double the value.Cut the figure by the rectangle with small width. Then the area of the rectangle is given by 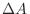 and
and
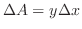
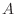 is
is
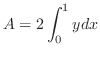
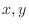 are parameterized by
are parameterized by 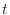 .
.
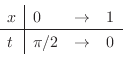
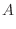 |
 |
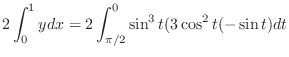 |
|
 |
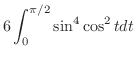 |
||
 |
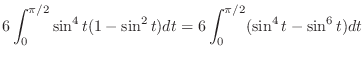 |
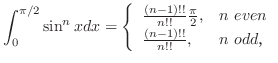
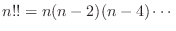 .
Therefore,
.
Therefore,
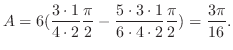
2.
(a)
Cut this figure by the plane perpendicular to the axis of rotation. Then its cross section becomes a shape called a washer.
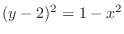 implies
implies
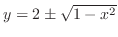 .Then
.Then
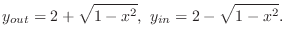
 is
is
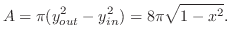
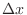 . Then the volume
. Then the volume 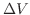 is
is
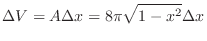
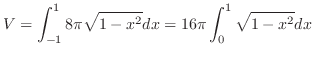
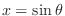 ,we have
,we have
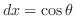 ,
,
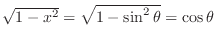 . Therefore,
. Therefore,
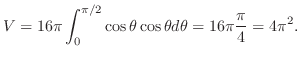
(b)
The graph of this function is called a cycloid.The intersection with the  axis is when
axis is when 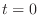 and
and 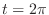 . When this figure is rotated around the
. When this figure is rotated around the  axis and the rotating body is cut by a plane perpendicular to the
axis and the rotating body is cut by a plane perpendicular to the  axis, the cross-sectional area is
axis, the cross-sectional area is 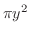 . If you add a little thickness
. If you add a little thickness 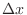 to this, its volume will be
to this, its volume will be
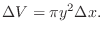
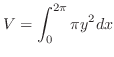
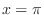
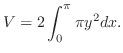
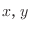 by the parameter
by the parameter 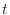 . Then
. Then
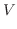 |
 |
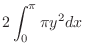 |
|
 |
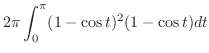 |
||
 |
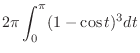 |
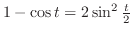 , we have
, we have
 |
 |
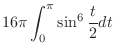 |
|
 |
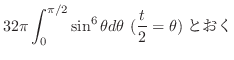 |
||
 |
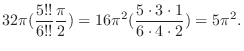 |
3.
(a)
The graph of
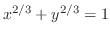 is called asteroid.Now parametrize this function. Then
is called asteroid.Now parametrize this function. Then
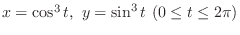 .
Then we calculate the length of the section
.
Then we calculate the length of the section
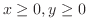 . Then multiply by 4. A part of curve
. Then multiply by 4. A part of curve 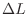 is given by
is given by
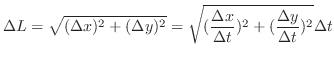
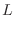 |
 |
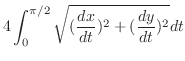 |
|
 |
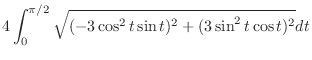 |
||
 |
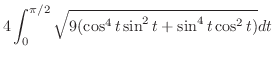 |
||
 |
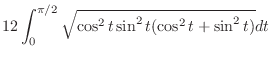 |
||
 |
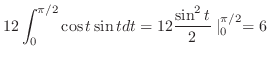 |
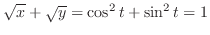
 |
 |
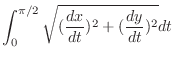 |
|
 |
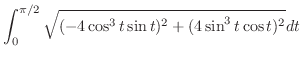 |
||
 |
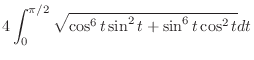 |
||
 |
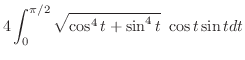 |
||
 |
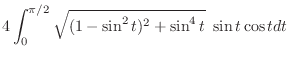 |
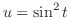 . Then
. Then
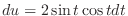 .Note that
.Note that
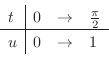
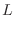 |
 |
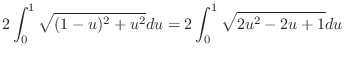 |
|
 |
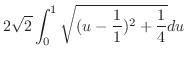 |
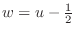 とおくと
とおくと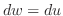
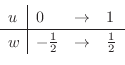
 |
 |
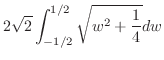 |
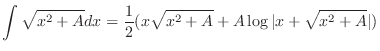
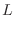 |
 |
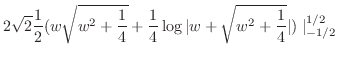 |
|
 |
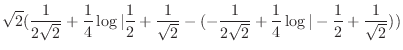 |
||
 |
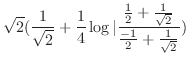 |
||
 |
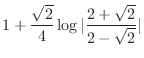 |
||
 |
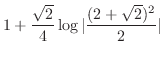 |
||
 |
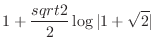 |
(c)
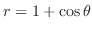 is symmetric with
is symmetric with  -axis and,
-axis and,
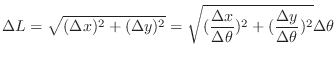
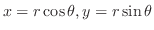 .Then
.Then
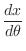 |
 |
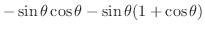 |
|
 |
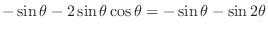 |
||
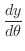 |
 |
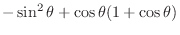 |
|
 |
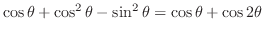 |
 |
 |
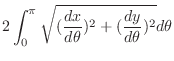 |
|
 |
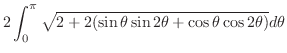 |
||
 |
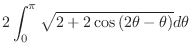 |
||
 |
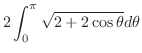 |
||
 |
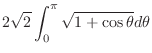 |
||
 |
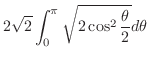 |
||
 |
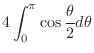 |
||
 |
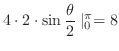 |