Next: Applications of definite integral Up: INTEGRATION Previous: Extension of definite integrals
3.9
1.
Note that we use the following symbols.
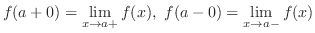
(a)
To integrate
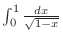 , we need to know
, we need to know
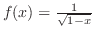 is continuous on
is continuous on 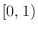 .
.
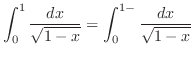
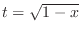 . Then
. Then 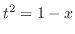 and
and
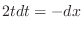 .Note that
.Note that
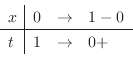
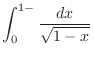 |
 |
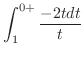 |
|
 |
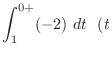 is never 0 is never 0 |
||
 |
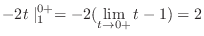 |
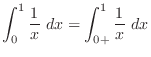
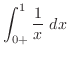 |
 |
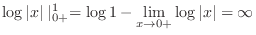 |
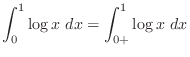
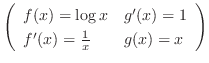
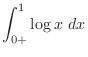 |
 |
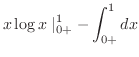 |
|
 |
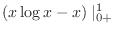 |
||
 |
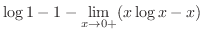 |
||
 |
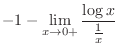 |
||
 |
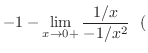 L'Hospital's rule L'Hospital's rule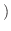 |
||
 |
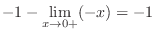 |
2.
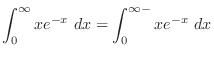
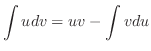
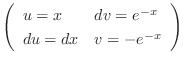
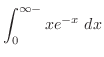 |
 |
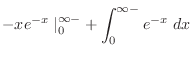 |
|
 |
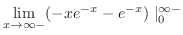 |
||
 |
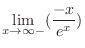 |
||
 |
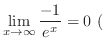 L'Hospital's rule L'Hospital's rule |
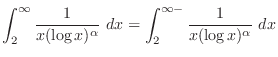
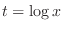 . Then
. Then
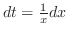 .Note that
.Note that
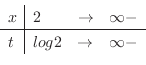
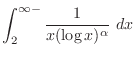 |
 |
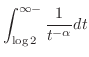 |
|
 |
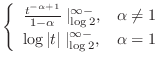 |
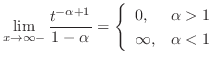
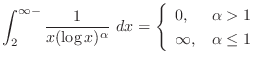
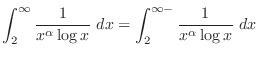
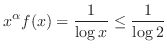
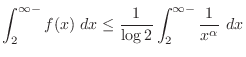
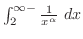 converges at
converges at
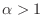 .
For
.
For
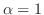 ,we let
,we let
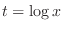 . Then
. Then
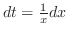 .Note that
.Note that
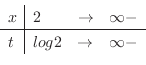
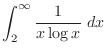 |
 |
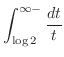 |
|
 |
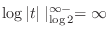 |
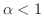 and
and
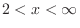 ,
,
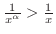 implies that
implies that
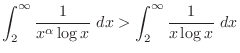
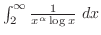 diverges.
diverges.
3.
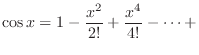
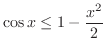
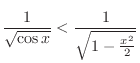
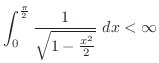
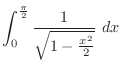 |
 |
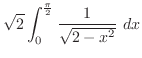 |
|
 |
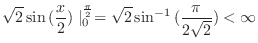 |
(b) 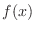 is continuous on
is continuous on ![$(0,1]$](img1414.png) .Let
.Let
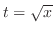 . Then
. Then 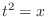 and
and 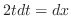 .Note that
.Note that
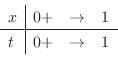
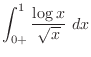 |
 |
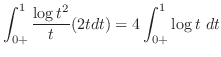 |
|
 |
![$\displaystyle 4[t\log{t} - t\mid_{0+}^{1} = 4[\log{1} - 1 - \lim_{t \to 0+}(t\log{t} - t)]$](img1471.png) |
||
 |
![$\displaystyle 4[-1 - \lim_{t \to 0+}(\frac{\log{t} -1}{\frac{1}{t}})]$](img1472.png) |
||
![$\displaystyle 4[-1 - \lim_{t \to 0+}\frac{1/t}{-1/t^2} ] = -4$](img1473.png) |