Next: Sequences Up: FUNCTIONS Previous: Continuous functions
1.5
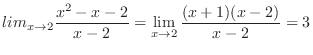
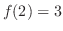 . Then
. Then 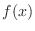 is continuous at
is continuous at 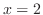 .
.
For
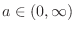 , we show
, we show
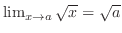 DFor any
DFor any
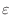 Cwe set
Cwe set
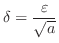 . Then
. Then
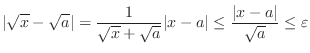
3.
(a)
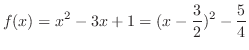 . Then the maximum is at
. Then the maximum is at 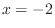 and
and 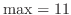 . Also, the minimum is at
. Also, the minimum is at 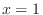 and
and 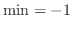
(b)
As 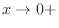 ,
,
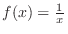 approaches to
approaches to 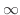 . Then no maximum and
. Then no maximum and 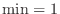
Let
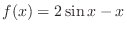 . Then
. Then 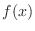 is continuous on
is continuous on
![$\displaystyle{[\frac{\pi}{2},\pi]}$](img244.png) . Since
. Since
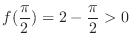 and
and
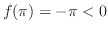 . Thus by the mean-value theorem, we have
. Thus by the mean-value theorem, we have 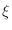 in
in
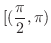 so that
so that
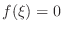 .
.