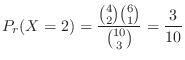Next: Gamma disttribution Up: Theoretical distribution Previous: Normal distribution Contents
When trials are repeated independently, the number of trials until just before the event of interest first occurs is  , and if
, and if 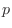 is the probability of the event of interest occurring, The probability of the event of interest
is the probability of the event of interest occurring, The probability of the event of interest 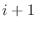 st time is
st time is
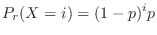
 should follow the geometric distribution
should follow the geometric distribution 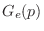 and denoted
and denoted
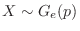
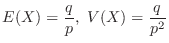
One way to find the expected value 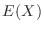 is to use a generating function.
is to use a generating function.
Discrete case
Let
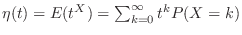 . Then
. Then
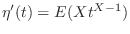 . Thus for,
. Thus for,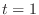 ,
,
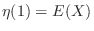 . Therefore, the expectation can be found if
. Therefore, the expectation can be found if 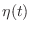 is found.
is found.
Continuous case
Let
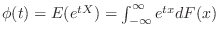 . Then express
. Then express 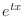 by the power series. Then
by the power series. Then
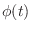 |
 |
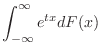 |
|
 |
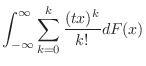 |
||
 |
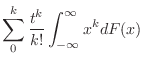 |
||
 |
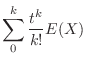 |
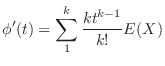
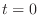 . Then
. Then
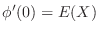
Hypergeometric distribution There are  white balls and
white balls and 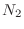 black balls in the jar. Let
black balls in the jar. Let  be the number of white balls when taking out
be the number of white balls when taking out 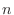 balls one by one without undoing (non-restoration extraction). The probability that the number of white balls is
balls one by one without undoing (non-restoration extraction). The probability that the number of white balls is 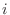 is given by
is given by
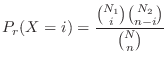
 follows the hypergeometric distribution and denoted by
follows the hypergeometric distribution and denoted by
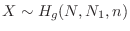
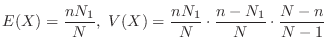
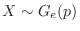 , show
, show
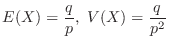
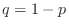 .
.
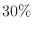 . On average, find out how many games you need to play to win for the first time.
. On average, find out how many games you need to play to win for the first time.
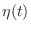 |
 |
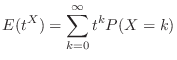 |
|
 |
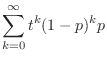 |
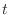 .
.
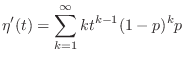
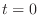 . Then
. Then
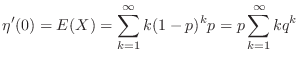
Let
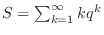 . Then find
. Then find
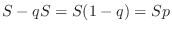
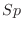 |
 |
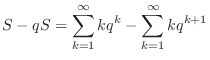 |
|
 |
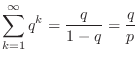 |
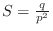 and
and
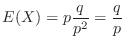
(b) Let  be the numbr of games to play to win the first time. Then
be the numbr of games to play to win the first time. Then
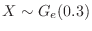 .Thus the number of games to play to win the first time is
.Thus the number of games to play to win the first time is 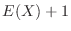
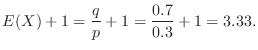
(c) If  is the number of winning lottery,
is the number of winning lottery,
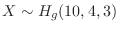 . Therefore, if you draw 3 lots, the probability of winning 2 of them is
. Therefore, if you draw 3 lots, the probability of winning 2 of them is