Next: About this document ... Up: Theoretical distribution Previous: Geometric distribution Contents
1. Suppose that the amount of gasoline  kiloliter sold per week in a gas station follows a distribution with the following density function.
kiloliter sold per week in a gas station follows a distribution with the following density function.
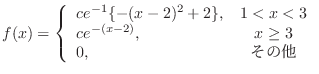
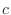 .
.
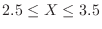 .
.
2. The blood types of Japanese are said to be A type 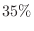 , B type
, B type 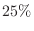 , AB type
, AB type 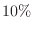 , and O type
, and O type 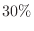 . Now, when there are four people, find the probability that all four people have different blood types.
. Now, when there are four people, find the probability that all four people have different blood types.
3.. It is assumed that the telephone talk time follows an exponential distribution of 2 minutes on average. Find the probability that you will have to wait at least 10 minutes when there are 3 people in the phone box, including those who are already busy.
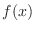 a density function,
a density function,
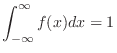
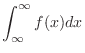 |
 |
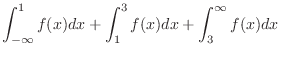 |
|
 |
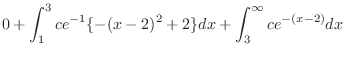 |
||
 |
![$\displaystyle ce^{-1}\left[-\frac{1}{3}(x-2)^{3} + 2x \right]_{1}^{3} - \left[ce^{-(x-2)}\right]_{3}^{\infty}$](img624.png) |
||
 |
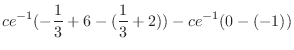 |
||
 |
2. Let 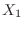 be the number of people with blood type A,
be the number of people with blood type A,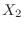 be the numbeBr of people with blood type ,
be the numbeBr of people with blood type ,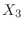 be the number of people with blood type AB,
be the number of people with blood type AB,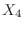 be the number of people with blood type O. Then
be the number of people with blood type O. Then
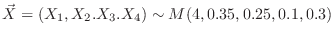 .Thus,
.Thus,
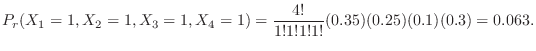
3. Let
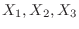 be the talk time of 3 people. Then
be the talk time of 3 people. Then
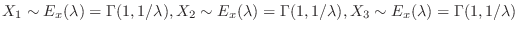 .Now let
.Now let
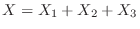 . Then
. Then  represents the total talk time of 3 people.Thus,
represents the total talk time of 3 people.Thus,
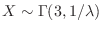 .Also,
.Also,
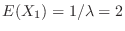 implies
implies
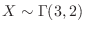 .Thus, the probability of having to wait more than 10 minutes is
.Thus, the probability of having to wait more than 10 minutes is
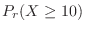 |
 |
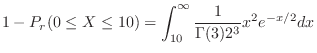 |
|
 |
![$\displaystyle 1 - \frac{1}{16}\int_{0}^{10}x^2 e^{-x/2}dx = 1 - [-2x^2 e^{-x/2}\mid_{0}^{10} + 4\int_{0}^{10}xe^{-x/2}dx ]$](img640.png) |
||
 |
![$\displaystyle 1 - \frac{1}{16}[-200e^{-5} + 4(-2xe^{-x/2}\mid_{0}^{10} + 2\int_{0}^{10}e^{-x/2}dx)]$](img641.png) |
||
 |
![$\displaystyle 1 - \frac{1}{16}[-200e^{-5} -80e^{-5} - 16e^{-x/2}\mid_{0}^{10}] = 1 - \frac{1}{16}[-296e^{-5} + 16] = \frac{296 e^{-5}}{16} = 0.1246$](img642.png) |