Next: Geometric distribution Up: Theoretical distribution Previous: Poisson distribution Contents
The probability density function of the random variable  is given by
is given by
![$\displaystyle g(x) = \frac{1}{\sqrt{2\pi} \sigma} EXP\left[-\frac{(x-\mu)^2}{2 \sigma^2}\right], \ -\infty < x < \infty $](img489.png)
 follows the normal distribution and write
follows the normal distribution and write
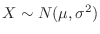 .
.
Also,the value of
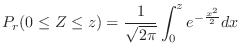
Normalization
Converting the mean 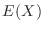 of the random variable
of the random variable  to 0 and the variance
to 0 and the variance 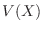 to 1 is called normalization.
Normalization method
Let
to 1 is called normalization.
Normalization method
Let
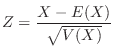
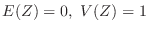
1. For
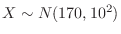 , find the following probabilities..
, find the following probabilities..
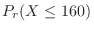
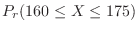
2. For
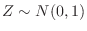 , find the
, find the 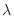 satisfying the followings.
satisfying the followings.
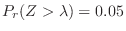
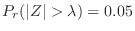
3. The height of boys at the age of 20 nationwide shall follow the normal distribution
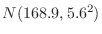 .
.
4. The following can be said about the binomial distribution, Poisson distribution, and normal distribution.
For
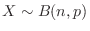 ,
,
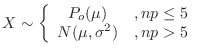
Using this, answer the following questions.
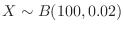 ,find
,find
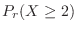 .
.
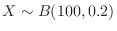 ,find
,find
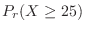 .
.
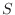 is 90 or more and 100 or less.
is 90 or more and 100 or less.
1. Since
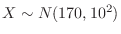 ,let
,let
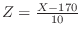 . then
. then
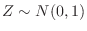 .
.
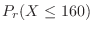 |
 |
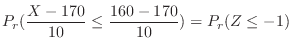 |
|
 |
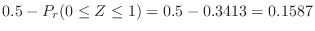 |
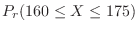 |
 |
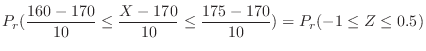 |
|
 |
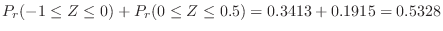 |
2.
Find 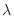 satisfying
satisfying
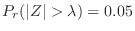 .
According to the standard normal distribution table, the value of
.
According to the standard normal distribution table, the value of
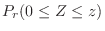 is given. Then we write
is given. Then we write
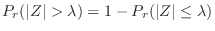
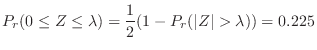
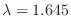 .
.
Find the 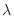 so that
so that
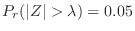 . According to the standard normal distribution table, we can find the value of
. According to the standard normal distribution table, we can find the value of
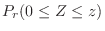 . Rewrite
. Rewrite
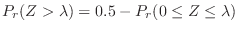
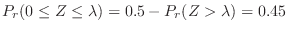
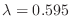 .
.
3.
Normalized from mean 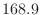 , variance
, variance 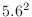 ,
,
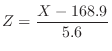
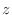 so that
so that
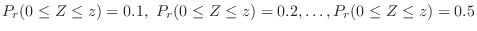
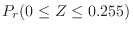 |
 |
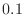 |
|
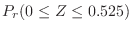 |
 |
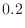 |
|
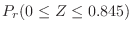 |
 |
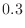 |
|
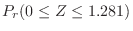 |
 |
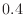 |
|
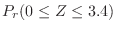 |
 |
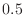 |
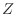 as follows.
as follows.
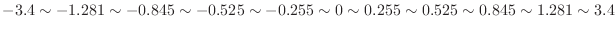
Let 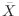 be the average height of 120 persons. Thenby the central limit theorem,
be the average height of 120 persons. Thenby the central limit theorem,
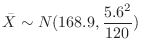
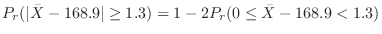
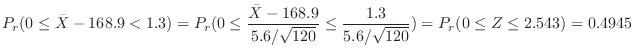
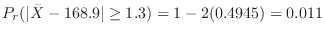
4.
Since
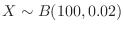 ,
,
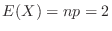 . Then we can approximate with the Poisson distribution. Note that
. Then we can approximate with the Poisson distribution. Note that
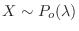 ,
,
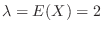 . Then
. Then
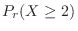 |
 |
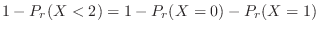 |
|
 |
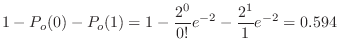 |
Since
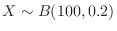 ,
,
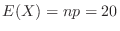 . Then we approximae using the normal distribution.
. Then we approximae using the normal distribution.
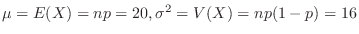 implies
implies
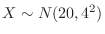 . Thus
. Thus
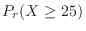 |
 |
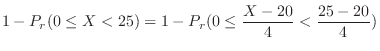 |
|
 |
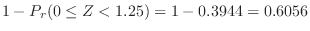 |
Let  be the number of 1 rolls. Then
be the number of 1 rolls. Then
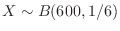 . Then find the probability that
. Then find the probability that 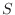 is 90 or more and 100 or less.
is 90 or more and 100 or less.
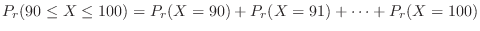
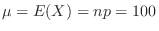 ,
,
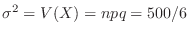 ,
,
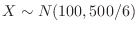 . Using the standard distribution,
. Using the standard distribution,
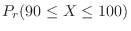 |
 |
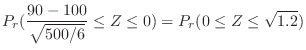 |
|
 |
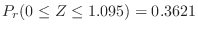 |
If  is the number of times the eye head appears, it follows the binomial distribution of
is the number of times the eye head appears, it follows the binomial distribution of
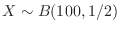 . Therefore, if the probability that the number of times the head comes out is 40 or more and 60 or less is calculated,
. Therefore, if the probability that the number of times the head comes out is 40 or more and 60 or less is calculated,
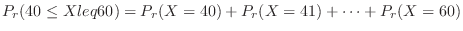
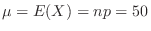 ,
,
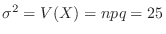 ,
,
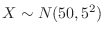 . Using the standard distribution,
. Using the standard distribution,
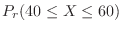 |
 |
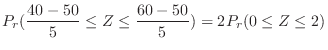 |
|
 |
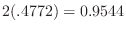 |