DeMoivre's theorem and Euler's formula

Exercise1.2

1. Prove De Moivre's theorem 2. Simplify the following complex numbers.

(a)

$\left(\frac{1 - i}{\sqrt{2}}\right)^{7}$

(b)

$(\sqrt{3} - i)^{6}$

(c)

$\frac{(1 + \sqrt{3}i)^{6}}{(-1 + i)^{10}}$

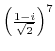
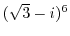
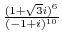
3. Solve the following equation.

(a)

$z^2 = i$

(b)

$z^3 = -1$

(c)

$z^4 = -1 + \sqrt{3}i$

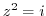
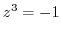
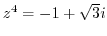
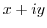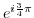
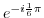
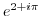
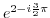
4. Express the followings in the form of $x + iy$.

(a)

$e^{i\frac{3}{4}\pi}$

(b)

$e^{-i\frac{1}{6}\pi}$

(c)

$e^{2 + i\pi}$

(d)

$e^{2- i\frac{3}{2}\pi}$

5. Express the followings in the polar form $re^{i\theta}$.

(a)

$-2$

(b)

$i$

(c)

$1+i$

(d)

$\sqrt{3} - i$

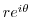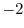
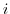
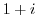
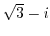
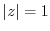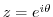(6) Show that $\vert z\vert = 1$ if and only if $z = e^{i\theta}$.