Next: 2.1 Complex function Up: Solution Previous: 1.1 Complex numbers and Index
1.
By Euler's formula,
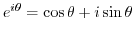 . Thus for all real numbers
. Thus for all real numbers 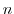 ,
,
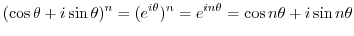
2.
(a) If it contains exponentiation, it is recommended to change the inside of parentheses to polar form once.
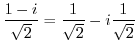
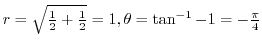 . Thus
. Thus
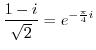
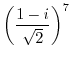 |
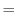 |
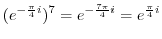 |
|
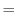 |
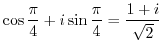 |
(b) If it contains exponentiation, it is recommended to change the inside of parentheses to polar form once.
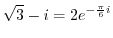
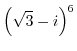 |
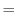 |
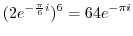 |
|
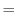 |
![$\displaystyle 64[\cos{\pi} - i \sin{\pi}] = -64$](img248.png) |
(c) If it contains exponentiation, it is recommended to change the inside of parentheses to polar form once.
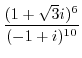 |
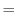 |
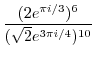 |
|
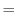 |
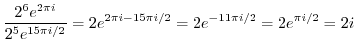 |
3.
(a) Use the root formula of the quadratic equation
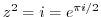 implies
implies
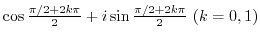
(b) Use the root formula of the quadratic equation
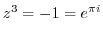 implies
implies
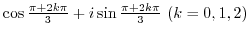
(c) Use the root formula of the quadratic equation
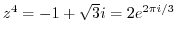 implies
implies
![$2^{1/4}[\cos{\frac{2\pi/3 + 2k\pi}{4}} + i\sin{\frac{2\pi/3 + 2k\pi}{4}}] (k = 0,1,2,3)$](img257.png)
4.
(a) To convert from polar coordinates to Cartesian coordinates, use
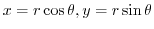 .
.
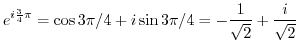
(b) To convert from polar coordinates to Cartesian coordinates, use
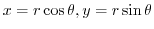 .
.
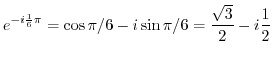
(c) To convert from polar coordinates to Cartesian coordinates, use
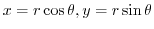 .
.
![$\displaystyle e^{2 + i\pi} = e^2 e^{i \pi} = e^{2}[\cos{\pi} + i \sin{\pi} ]= -e^{2}$](img261.png)
(d) To convert from polar coordinates to Cartesian coordinates, use
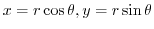 .
.
![$\displaystyle e^{2 - i\frac{3}{2}\pi} = e^2 e^{-i\frac{3}{2}\pi} = e^{2}[\cos{3\pi/2} - i \sin{3\pi/2}]= e^{2}i$](img262.png)
5.
(a) To convert from Cartesian coordinates to polar coordinates, we use
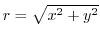 ,
,
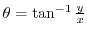 for
for
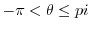 .
.
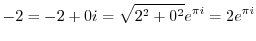
(b) To convert from Cartesian coordinates to polar coordinates, use
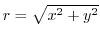 ,
,
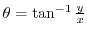 for
for
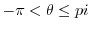 .
.
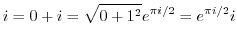
(c) To convert from Cartesian coordinates to polar coordinates, use
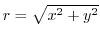 ,
,
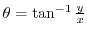 for
for
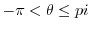 .
.
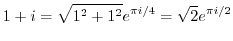
(d) To convert from Cartesian coordinates to polar coordinates, use
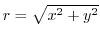 ,
,
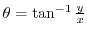 縺溘□縺97,
縺溘□縺97,
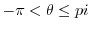 .
.
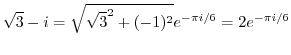
Let
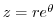 . Then since
. Then since 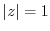 , we have
, we have
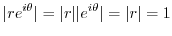
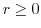 implies
implies 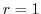 and
and
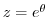 .
.
Next, if
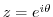 , then show
, then show 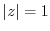 .
.