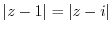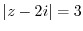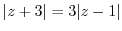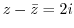Next: DeMoivre's theorem and Euler's Up: Complex numbers Previous: Complex numbers Index
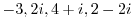 on the complex plane
2. Prove the following theorem.
on the complex plane
2. Prove the following theorem.
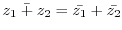
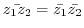
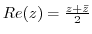
3. Prove the following inequality.
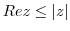
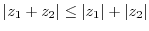
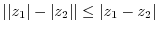
4. Express the following complex numbers in polar form.
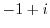
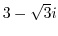
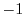
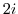
5. Draw a curve that satisfies the following equation.
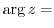 constant
constant
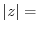 constant
constant