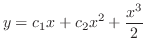Next: 演習問題2.6 Up: 線形微分方程式(linear differential equations) Previous: 演習問題2.5 目次 索引
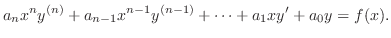
話をわかりやすくするため2階の場合を考えます.
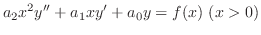
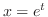 とおいて独立変数を
とおいて独立変数を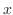 から
から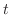 に変換します.
に変換します.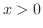 より
より
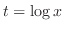 なので
なので
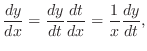
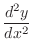 |
 |
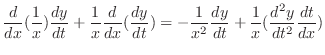 |
|
 |
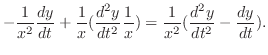 |
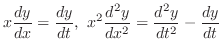
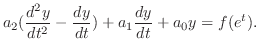
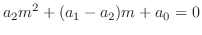
じつは決定方程式は簡単に求めることができます.微分方程式
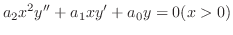
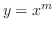 を代入するだけでよいのです.
を代入するだけでよいのです.
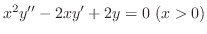 を解け.
を解け.
解
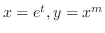 とおくと,決定方程式は
とおくと,決定方程式は
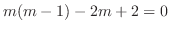 となり,根は
となり,根は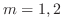 である.決定方程式は微分方程式
である.決定方程式は微分方程式
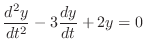
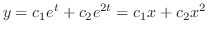

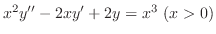 を解け.
を解け.
解
変数変換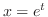 より,与えられた方程式は
より,与えられた方程式は
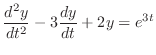
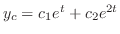 である.次に
である.次に
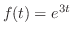 より,特殊解を未定係数法で求める.
より,特殊解を未定係数法で求める.
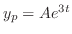 を
を
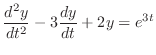
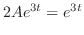
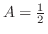 となり一般解
となり一般解
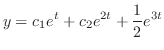
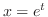 を元に戻すと与えられた方程式の一般解
を元に戻すと与えられた方程式の一般解