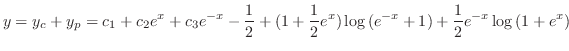Next: 演習問題2.5 Up: 線形微分方程式(linear differential equations) Previous: 演習問題2.4 目次 索引
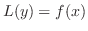 の特殊解を未定係数法により求めました.ただ残念なことにこの解法は
の特殊解を未定係数法により求めました.ただ残念なことにこの解法は が定数係数同次線形微分方程式の解の形をとっているときにしか使えませんでした.
が定数係数同次線形微分方程式の解の形をとっているときにしか使えませんでした.
ここでは階数低減法と同じように,どの線形微分方程式
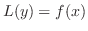 にも用いることができる定数変化法(variation of parameter)とよばれている解法を学びます.
にも用いることができる定数変化法(variation of parameter)とよばれている解法を学びます.
階数低減法では対応する同次線形微分方程式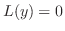 のひとつの解から
のひとつの解から
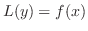 の一般解を求めました.もし同次線形微分方程式の基本解がわかっていたらどうでしょう.多分もっと簡単に一般解が求められてもよいでしょう.このことを2階の線形微分方程式を例にとって考えてみましょう.
の一般解を求めました.もし同次線形微分方程式の基本解がわかっていたらどうでしょう.多分もっと簡単に一般解が求められてもよいでしょう.このことを2階の線形微分方程式を例にとって考えてみましょう.
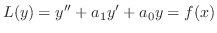
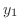 と
と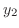 は
は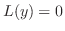 の基本解だとします.ここで
の基本解だとします.ここで
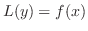 の特殊解を
の特殊解を
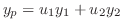
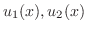 は後で定める未定関数です.2つの関数を決めなければならないので,2つの条件が必要となります.最初の条件は
は後で定める未定関数です.2つの関数を決めなければならないので,2つの条件が必要となります.最初の条件は
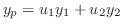 が
が
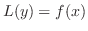 の解であることです.2つめの条件は計算を簡単にするために設けた条件
の解であることです.2つめの条件は計算を簡単にするために設けた条件
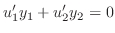
最初の条件を用いるため,
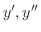 を求め
を求め
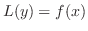 に代入すると
に代入すると
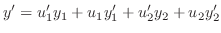
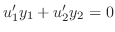 を用いると
を用いると
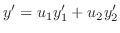
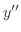 を求めると
を求めると
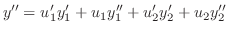
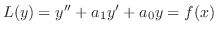 に代入すると
に代入すると
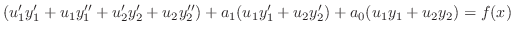
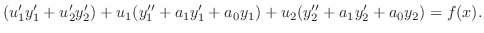
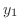 と
と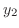 は
は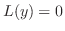 の解より
の解より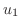 と
と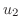 の係数は0です.したがって
の係数は0です.したがって
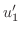 と
と
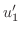 は連立方程式
は連立方程式
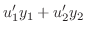 |
 |
0 | |
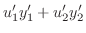 |
 |
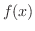 |
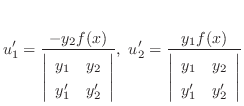
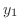 と
と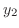 のWronskiの行列式です.また
のWronskiの行列式です.また
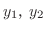 は一次独立なので定理2.4よりWronskiの行列式は0になりません.よって
は一次独立なので定理2.4よりWronskiの行列式は0になりません.よって
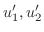 を求めることができ,これより
を求めることができ,これより
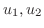 ひいては
ひいては
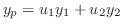 を求めることができます.
を求めることができます.
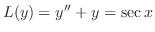 を求めよ.
を求めよ.
解
補助方程式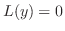 の特性方程式は
の特性方程式は
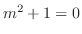 より特性根
より特性根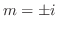 を得る.よって余関数は
を得る.よって余関数は
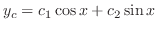
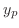 を求める.定数変化法より
を求める.定数変化法より
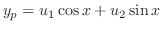
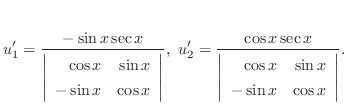
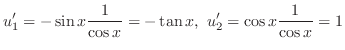
 定数無視
定数無視
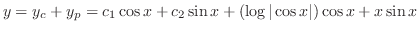

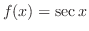 なのでこの例題には未定係数法は使えませんでした.次に
なのでこの例題には未定係数法は使えませんでした.次に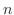 階線形微分方程式への定数変化法の用い方を考えてみます.
階線形微分方程式への定数変化法の用い方を考えてみます.
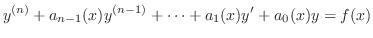
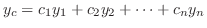
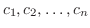 を変数
を変数
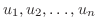 で置き換えると特殊解
で置き換えると特殊解
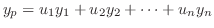
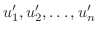 は連立方程式
は連立方程式
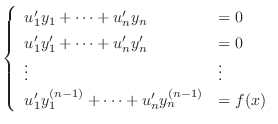
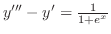 を解け.
を解け.
解
補助方程式
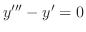 の特性方程式は
の特性方程式は
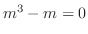 より特性根
より特性根
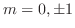 を得る.よって余関数は
を得る.よって余関数は
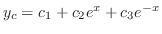
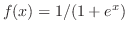 なので定数変化法を用いて特殊解を求める.
なので定数変化法を用いて特殊解を求める.
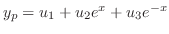
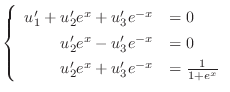
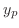 を見つける.Cramerの公式より
を見つける.Cramerの公式より
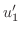 |
 |
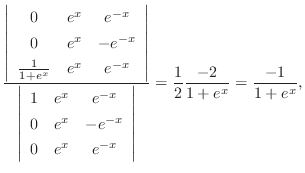 |
|
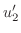 |
 |
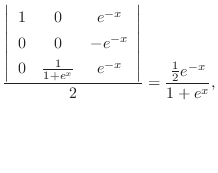 |
|
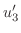 |
 |
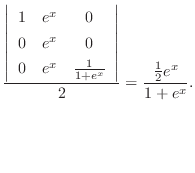 |
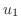 |
 |
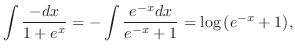 |
|
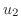 |
 |
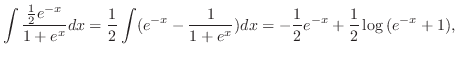 |
|
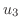 |
 |
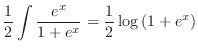 |
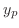 に戻すと一般解
に戻すと一般解