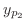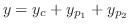Next: 演習問題2.1 Up: 線形微分方程式(linear differential equations) Previous: 線形微分方程式(linear differential equations) 目次 索引
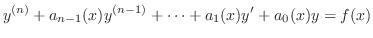
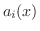 を 係数関数(coefficient function),
を 係数関数(coefficient function), を入力関数(input function)といいます.
を入力関数(input function)といいます.
 のときこの方程式を同次方程式(homogeneous equation)といいます.この微分方程式の左辺を
のときこの方程式を同次方程式(homogeneous equation)といいます.この微分方程式の左辺を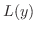 と省略した形で表わすことがよくあります.こうすると高階線形微分方程式は
と省略した形で表わすことがよくあります.こうすると高階線形微分方程式は
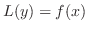
 は微分作用素(differential operator)とよばれ線形性をもっています.つまり任意の関数
は微分作用素(differential operator)とよばれ線形性をもっています.つまり任意の関数
 と任意の定数
と任意の定数
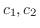 に対して
に対して
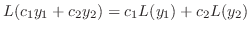
 の線形性から次の定理が得られます.
の線形性から次の定理が得られます.
|
定理 2..1 同次方程式の解の集合はベクトル空間をなす.
|
証明を行なう前にベクトル空間の復習をしておきます.
ベクトル空間
2つの幾何ベクトルの和(vector addition)は,一方の幾何ベクトルの尻尾(始点)をもう一方の幾何ベクトルの頭(終点)につけることにより定義されます.よって2つの幾何ベクトルの和は最初の幾何ベクトルの尻尾から次の幾何ベクトルの頭を結んだ有向線分で表わせます.ほかの見方をすると,2つの幾何ベクトルA,Bの和A  BはAとBによって作られる平行四辺形の対角線として表わせます.
BはAとBによって作られる平行四辺形の対角線として表わせます.
幾何ベクトルの和は次のような性質をもっています.各自確かめておいて下さい.
1.2つの幾何ベクトルの和はまた幾何ベクトルである.(このことを和は閉じているといいます)
2.任意の幾何ベクトルAとBにおいて,A+B = B+Aが成り立つ.(交換法則)
3.任意の幾何ベクトルA,B,Cにおいて,(A+B)+C = A+(B+C)が成り立つ.(結合法則)
4.任意の幾何ベクトルAに対して,A+0 = Aとなる幾何ベクトル0が存在する.(零元の存在)
5.任意の幾何ベクトルAに対して,A+B = 0となる幾何ベクトルBが存在する.(逆元の存在)
幾何ベクトルのスカラー倍 (scalar multiplication) 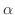 Aは幾何ベクトルAを実数
Aは幾何ベクトルAを実数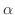 の大きさ
の大きさ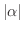 倍することで定義されます.ただし,
倍することで定義されます.ただし,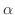 が負のときは方向が反対になります.幾何ベクトルのスカラー倍は次のような性質をもっています.各自確かめておいて下さい.
が負のときは方向が反対になります.幾何ベクトルのスカラー倍は次のような性質をもっています.各自確かめておいて下さい.
6.幾何ベクトルのスカラー倍はまた幾何ベクトルである.
7.任意の実数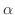 と
と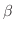 に対して,
に対して,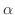 (
(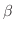 A) = (
A) = (
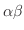 )Aが成り立つ.(結合法則)
)Aが成り立つ.(結合法則)
8.任意の実数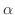 と
と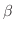 に対して,(
に対して,(
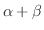 )A =
)A = 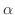 A +
A + 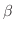 Aが成り立ち,任意の幾何ベクトルAとBに対して,
Aが成り立ち,任意の幾何ベクトルAとBに対して,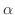 (A+B) =
(A+B) = 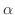 A +
A + 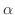 Bが成り立つ.(分配法則)
Bが成り立つ.(分配法則)
9.1A = A; 0A = 0; 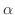 0 = 0が成り立つ.
0 = 0が成り立つ.
平面や空間の幾何ベクトルにおいて上の1から9までの性質が成り立ちます.このとき,平面や空間の幾何ベクトルの集まりを幾何ベクトル空間 (geometric vector space)といいます.幾何ベクトル空間はしばしばユークリッド空間ともよばれ,これから学ぶもっと抽象的なベクトル空間の特殊な場合です.一般に和およびスカラー倍が上の性質1から9を満たす物の集まりをベクトル空間(vector space)とよび,そこに含まれる物をベクトル(vector)といいます.よってこれから登場してくるベクトルには,幾何ベクトルに似ても似つかない物が沢山あります.
ここでは幾何ベクトル空間には似ても似つかないベクトル空間を紹介します.まず区間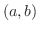 で連続な関数の集まりを
で連続な関数の集まりを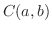 で表わし,区間
で表わし,区間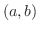 で区分的に連続な関数(piecewise continuous function)の集まりを
で区分的に連続な関数(piecewise continuous function)の集まりを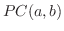 で表わします2.1. つまり
で表わします2.1. つまり
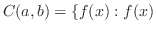 は
は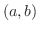 で連続},
で連続},
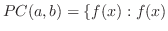 は区間
は区間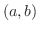 で区分的に連続}.
で区分的に連続}.
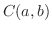 と
と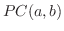 の
の と
と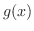 に対して,和およびスカラー倍を次のように定義します.
に対して,和およびスカラー倍を次のように定義します.
1.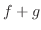 は点
は点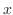 で
で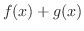 の値をとる関数.
の値をとる関数.
2.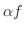 は点
は点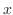 で
で
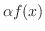 の値をとる関数.
の値をとる関数.
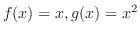 のとき,
のとき,
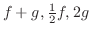 を求めよ.
を求めよ.
解
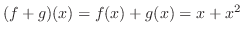
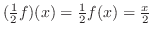
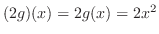

この和とスカラー倍によって,ベクトル空間になるための9個の性質が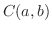 において成り立つことを示すのは,それほど難しくはないでしょう.よって
において成り立つことを示すのは,それほど難しくはないでしょう.よって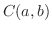 もベクトル空間となり,ベクトル空間に含まれる
もベクトル空間となり,ベクトル空間に含まれる や
や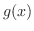 をベクトルとよぶことができます.幾何ベクトルと姿や形が違いますが立派なベクトルです.
をベクトルとよぶことができます.幾何ベクトルと姿や形が違いますが立派なベクトルです.
証明
同次方程式の解は明らかに微分可能.よって解の集合は連続な関数の集合の部分集合になる.したがって解の集合がベクトル空間となるためには,解の一次結合がまた解であることを示せばよい.そこで
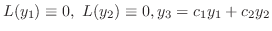 とおくと
とおくと
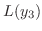 |
 |
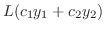 |
|
 |
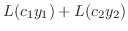 |
||
 |
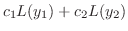 |
||
 |
0 |

同次方程式の解の集合はベクトル空間になるのでこれを解空間とよびます.次に一次独立という概念を取り入れるため,これから扱う同次方程式は区間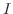 で連続な関数
で連続な関数
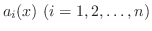 を係数とするものとします.
を係数とするものとします.
|
定理 2..2 同次方程式の解空間の基底は同次方程式を満たす
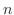 個の一次独立な関数である. 個の一次独立な関数である. |
解空間のすべてのベクトルを一次独立なベクトルの一次結合で表わせるとき,この一次独立なベクトルの集まりを解空間の基底といいます.また解空間の基底のことを基本解(fundamental solution)といいます.基底がわかれば解空間がわかるので,私たちは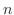 個の一次独立な解を見つければ,この定理よりすべての解を見つけたことになります.そこで
個の一次独立な解を見つければ,この定理よりすべての解を見つけたことになります.そこで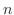 個の解が一次独立かどうかということは非常に大事になってきます.Wronskiはこの問題を解決するために次のような行列式を考えました.この行列式をWronskiの行列式(Wronskian determinant)といいます.
個の解が一次独立かどうかということは非常に大事になってきます.Wronskiはこの問題を解決するために次のような行列式を考えました.この行列式をWronskiの行列式(Wronskian determinant)といいます.
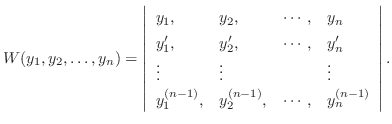
|
定理 2..3
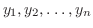 が区間 が区間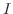 における同次方程式の解ならば における同次方程式の解ならば
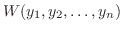 は は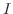 において恒等的に0か,けっして0にならないかのどちらかである.552 において恒等的に0か,けっして0にならないかのどちらかである.552 |
証明
(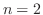 の場合)
の場合)
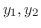 は
は
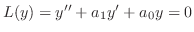 の解であるから,
の解であるから,
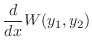 |
 |
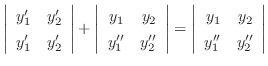 |
|
 |
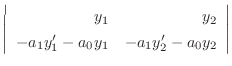 |
||
 |
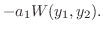 |
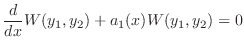
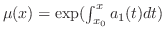 をかけると
をかけると
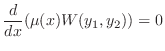
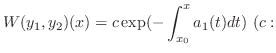 定数
定数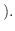
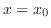 とおくと,
とおくと,
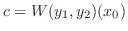 となり,
となり,
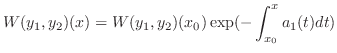

証明
( の場合)
の場合)
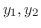 の一次結合を0とおくと
の一次結合を0とおくと
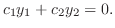
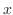 について微分すると
について微分すると
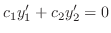
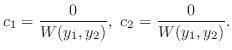
 が一次独立ならば,
が一次独立ならば,
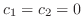 .つまり
.つまり
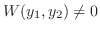 .また逆に,
.また逆に,
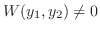 ならば,
ならば,
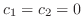 となり,
となり,
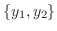 は一次独立.
は一次独立.

この2つの定理よりある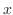 で
で
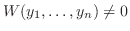 ならば,区間
ならば,区間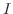 内のすべての
内のすべての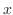 で
で
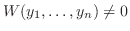 がいえます.
がいえます.
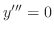 を解け.
を解け.
解
解空間は三次元で,
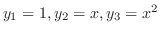 は明らかにこの微分方程式の解です.そこで一次独立か調べると
は明らかにこの微分方程式の解です.そこで一次独立か調べると
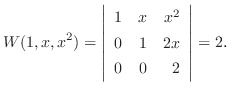
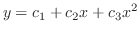

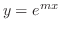 が
が
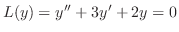 の解のとき,解空間の基底
の解のとき,解空間の基底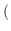 基本解
基本解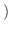 を求めよ.
を求めよ.
解
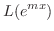 |
 |
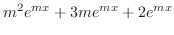 |
|
 |
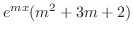 |
||
 |
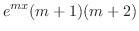 |
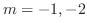 のとき,
のとき,
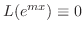 となる.また
となる.また
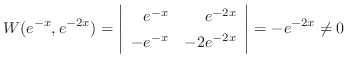
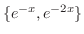 は解空間の基底(基本解)となる.
は解空間の基底(基本解)となる.

次に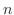 階の線形微分方程式の解について学びます.
階の線形微分方程式の解について学びます.
|
定理 2..5
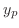 を を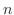 階線形微分方程式 階線形微分方程式
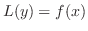 の特殊解, の特殊解,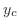 を同次方程式 を同次方程式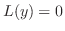 の一般解とすると, の一般解とすると,
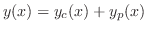 は は
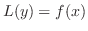 の一般解である. の一般解である. |
証明
仮定より
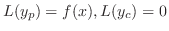 であるから,
であるから,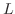 の線形性より
の線形性より
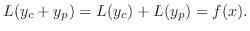
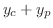 は
は
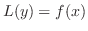 の解である.また
の解である.また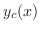 は
は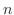 個の任意の定数を含んでいるので,
個の任意の定数を含んでいるので,
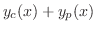 は一般解である.
は一般解である.

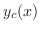 のことを余関数(complementary function)といいます.この定理より
のことを余関数(complementary function)といいます.この定理より
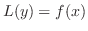 のひとつの特殊解がわかっているなら,一般解をみつけるには
のひとつの特殊解がわかっているなら,一般解をみつけるには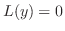 の余関数を見つければよいことがわかります.
の余関数を見つければよいことがわかります.
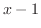 は
は
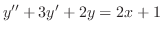 の解であることを示し,一般解を求めよ.
の解であることを示し,一般解を求めよ.
解
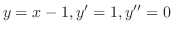 より
より
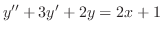 .また
.また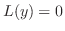 の解は例題2.2より
の解は例題2.2より
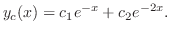
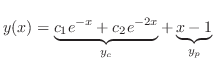

あるときは入力関数 が2つの関数
が2つの関数
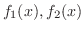 の和で与えられることもあります.こんなときは2つの方程式
の和で与えられることもあります.こんなときは2つの方程式
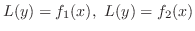 を考えると便利です.
を考えると便利です.
|
定理 2..6
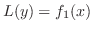 の解を の解を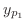 , ,
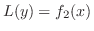 の解を の解を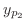 とすると, とすると,
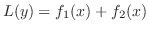 の解は の解は
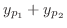 である.611 である.611 |
この定理は重ね合わせの原理(principle of superposition)といいます.この原理を使うと,たとえば
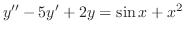
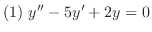 の解
の解
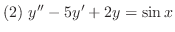 の解
の解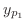
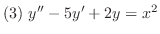 の解
の解