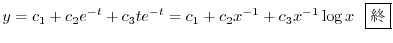Next: 3.1 解答 Up: 演習問題解答 Previous: 2.5 解答 索引
2.6
1.
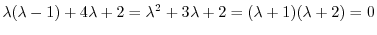
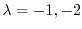 である.この決定方程式は次の微分方程式の特性方程式になっている.
である.この決定方程式は次の微分方程式の特性方程式になっている.
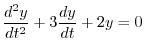
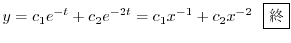
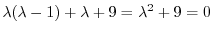
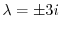 である.この決定方程式は
である.この決定方程式は
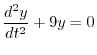
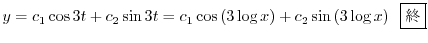
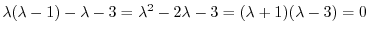
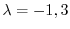 である.この決定方程式は次の微分方程式の特性方程式になっている.
である.この決定方程式は次の微分方程式の特性方程式になっている.
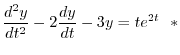
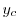 は
は
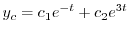
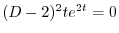 より
より
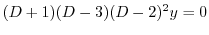
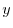 を求めると
を求めると
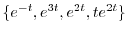 となるが,
となるが,
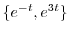 はすでに余関数に用いられているので省くと
はすでに余関数に用いられているので省くと
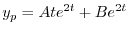
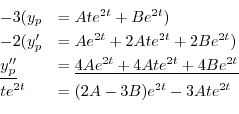
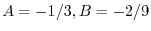 が求まり,
が求まり,
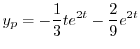
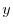 |
 |
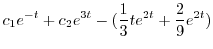 |
|
 |
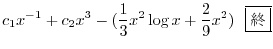 |
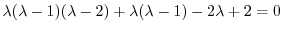
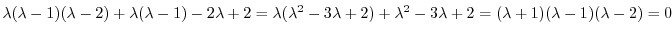
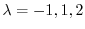 である.この決定方程式は次の微分方程式の特性方程式になっている.
である.この決定方程式は次の微分方程式の特性方程式になっている.
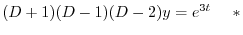
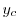 は
は
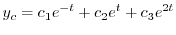
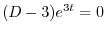 より
より
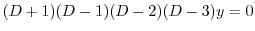
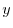 を求めると
を求めると
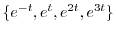 となるが,
となるが,
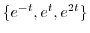 はすでに余関数に用いられているので省くと
はすでに余関数に用いられているので省くと
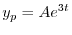
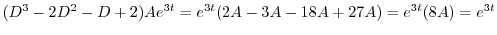
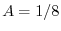 が求まり,
が求まり,
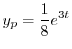
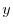 |
 |
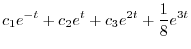 |
|
 |
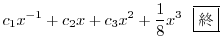 |
(e) 与式はEulerの方程式ではないが,両辺に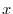 をかけることによりEulerの方程式に変形できる.
をかけることによりEulerの方程式に変形できる.
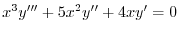
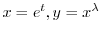 とおくと,決定方程式は
とおくと,決定方程式は
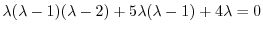
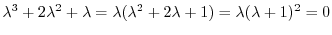
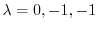 である.この決定方程式は次の微分方程式の特性方程式になっている.
である.この決定方程式は次の微分方程式の特性方程式になっている.