Next: 3.2 解答 Up: 演習問題解答 Previous: 2.6 解答 索引
3.1
1.
(a)
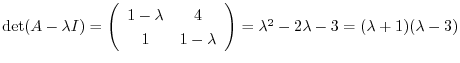 より固有値は
より固有値は
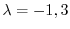 である.次に固有値
である.次に固有値
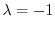 に対する固有ベクトル
に対する固有ベクトル は
は
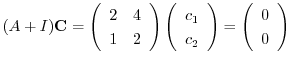
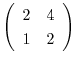 は被約階段行列
は被約階段行列
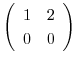 に変形されるので,
に変形されるので,
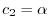 とおくと,
とおくと,
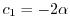 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
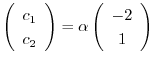 となり,
となり,
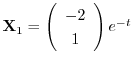 .
.
次に固有値
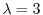 に対する固有ベクトルは
に対する固有ベクトルは
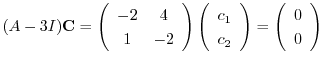
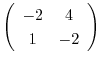 は被約階段行列
は被約階段行列
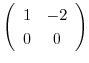 に変形されるので,
に変形されるので,
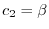 とおくと,
とおくと,
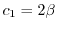 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
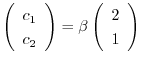 となり,
となり,
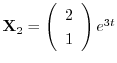 .
これより一般解は
.
これより一般解は
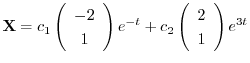

(b)
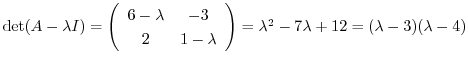 より固有値は
より固有値は
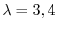 である.次に固有値
である.次に固有値
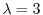 に対する固有ベクトルCは
に対する固有ベクトルCは
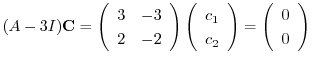
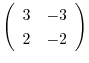 は被約階段行列
は被約階段行列
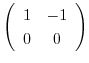 に変形されるので,
に変形されるので,
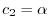 とおくと,
とおくと,
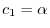 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
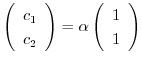 となり,
となり,
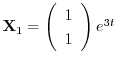 .
.
次に固有値
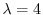 に対する固有ベクトルは
に対する固有ベクトルは
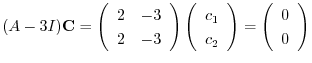
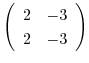 は被約階段行列
は被約階段行列
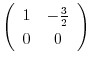 に変形されるので,
に変形されるので,
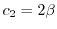 とおくと,
とおくと,
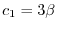 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
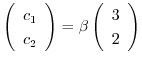 となり,
となり,
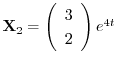 .
これより一般解は
.
これより一般解は
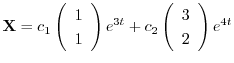

(c)
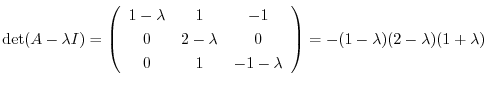 より固有値は
より固有値は
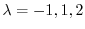 である.次に固有値
である.次に固有値
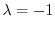 に対する固有ベクトル
に対する固有ベクトル は
は
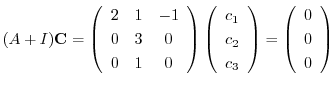
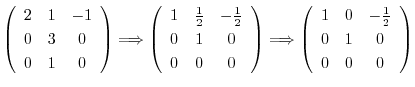
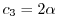 とおくと,
とおくと,
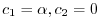 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
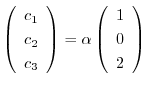 となり,
となり,
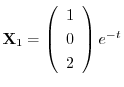 .
.
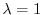 に対する固有ベクトルは
に対する固有ベクトルは
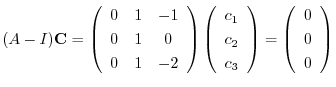
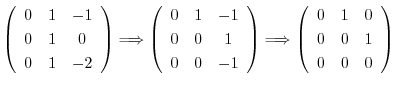
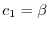 とおくと,
とおくと,
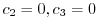 となるので固有ベクトルは
となるので固有ベクトルは
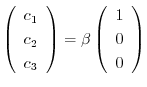 となり,
となり,
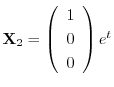 .
.
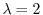 に対する固有ベクトルは
に対する固有ベクトルは
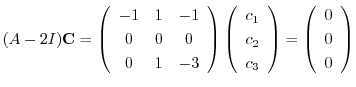
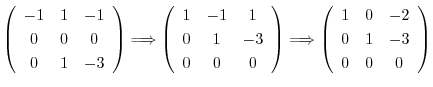
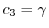 とおくと,
とおくと,
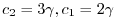 となるので固有ベクトルは
となるので固有ベクトルは
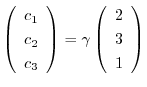 となり,
となり,
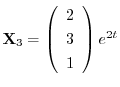 .
.
これより一般解は
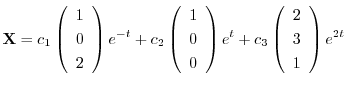

(d)
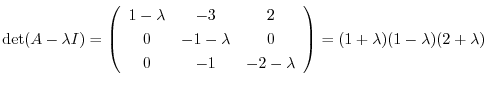 より固有値は
より固有値は
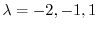 である.次に固有値
である.次に固有値
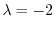 に対する固有ベクトル
に対する固有ベクトル は
は
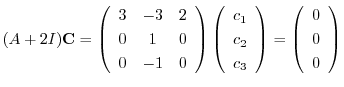
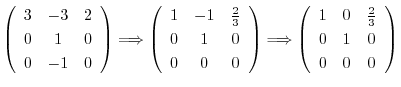
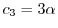 とおくと,
とおくと,
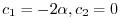 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
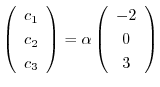 となり,
となり,
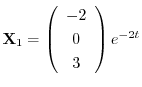 .
.
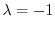 に対する固有ベクトルは
に対する固有ベクトルは
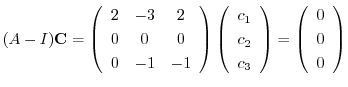
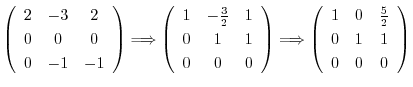
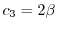 とおくと,
とおくと,
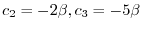 となるので固有ベクトルは
となるので固有ベクトルは
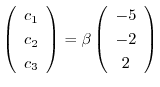 となり,
となり,
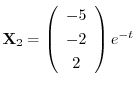 .
.
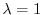 に対する固有ベクトルは
に対する固有ベクトルは
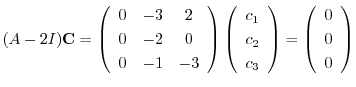
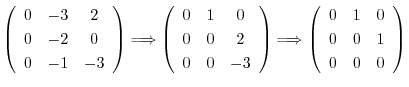
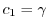 とおくと,
とおくと,
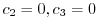 となるので固有ベクトルは
となるので固有ベクトルは
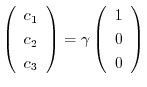 となり,
となり,
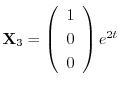 .
.
これより一般解は
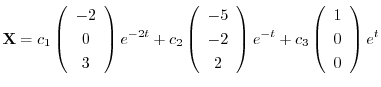

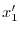 |
 |
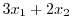 |
|
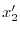 |
 |
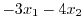 |
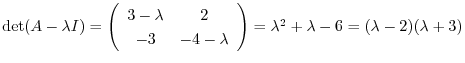 .
よって固有値は
.
よって固有値は
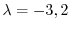 である.次に固有値
である.次に固有値
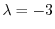 に対する固有ベクトル
に対する固有ベクトル は
は
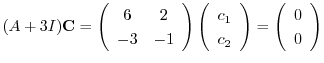
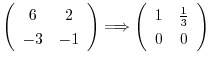
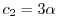 とおくと,
とおくと,
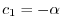 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
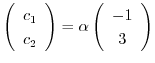 となり,
となり,
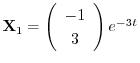 .
.
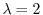 に対する固有ベクトルは
に対する固有ベクトルは
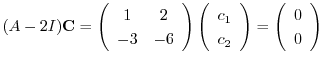
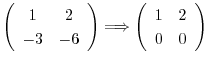
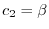 とおくと,
とおくと,
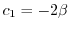 となるので固有ベクトルは
となるので固有ベクトルは
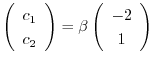 となり,
となり,
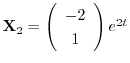 .
これより一般解は
.
これより一般解は
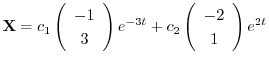

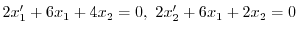
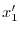 |
 |
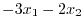 |
|
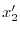 |
 |
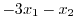 |
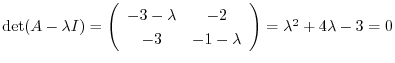 .
よって固有値は
.
よって固有値は
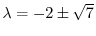 である.次に固有値
である.次に固有値
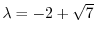 に対する固有ベクトル
に対する固有ベクトル を求める.
ここで行列
を求める.
ここで行列
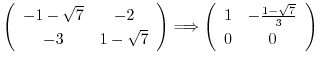
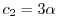 とおくと,
とおくと,
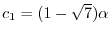 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
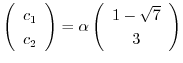 となり,
となり,
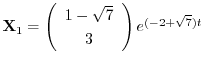 .
.
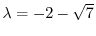 に対する固有ベクトルを求める.
行列
に対する固有ベクトルを求める.
行列
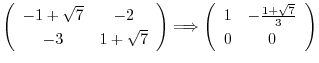 は被約階段行列に変形されるので,
は被約階段行列に変形されるので,
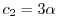 とおくと,
とおくと,
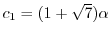 となる.したがって,固有ベクトルは
となる.したがって,固有ベクトルは
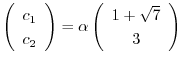 となり,
となり,
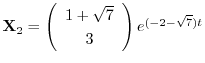 .
.
これより一般解は