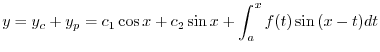Next: 2.6 解答 Up: 演習問題解答 Previous: 2.4 解答 索引
2.5
1.
(a) 補助方程式
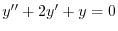 の特性方程式は
の特性方程式は
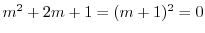 より特性根
より特性根
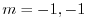 を得る.よって余関数は
を得る.よって余関数は
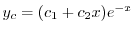
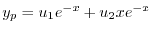
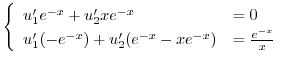
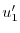 |
 |
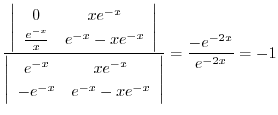 |
|
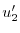 |
 |
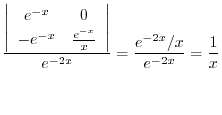 |
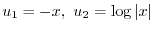 (定数無視)
(定数無視)
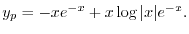
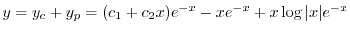

(b) 補助方程式
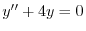 の特性方程式は
の特性方程式は
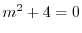 より特性根
より特性根
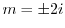 を得る.よって余関数は
を得る.よって余関数は
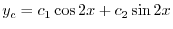
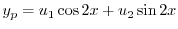
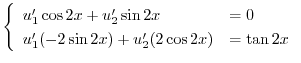
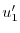 |
 |
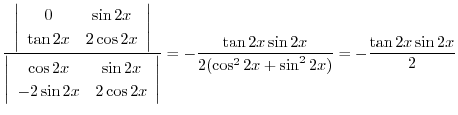 |
|
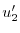 |
 |
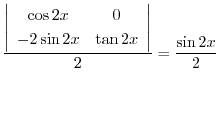 |
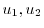 を求める.
を求める.
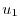 |
 |
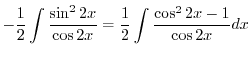 |
|
 |
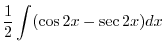 |
||
 |
 |
||
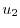 |
 |
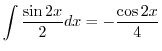 |
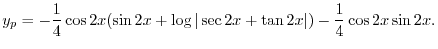
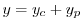 |
 |
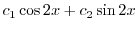 |
|
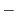 |
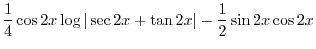 |

(c) 補助方程式
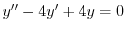 の特性方程式は
の特性方程式は
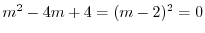 より特性根
より特性根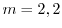 を得る.よって余関数は
を得る.よって余関数は
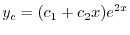
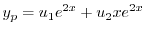
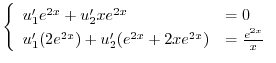
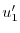 |
 |
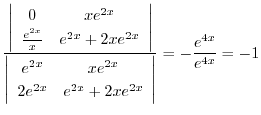 |
|
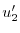 |
 |
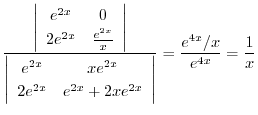 |
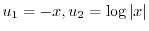 となるので,
となるので,
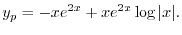
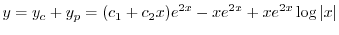

(d) 補助方程式
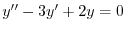 の特性方程式は
の特性方程式は
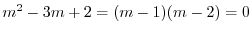 より特性根
より特性根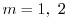 を得る.よって余関数は
を得る.よって余関数は
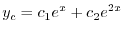
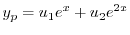
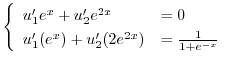
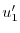 |
 |
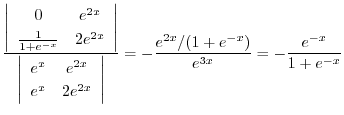 |
|
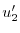 |
 |
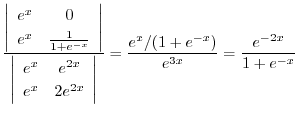 |
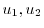 を求めると,
を求めると,
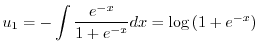
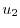 |
 |
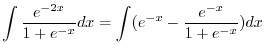 |
|
 |
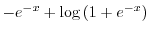 |
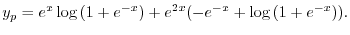
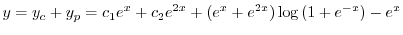

(e) 補助方程式
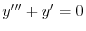 の特性方程式は
の特性方程式は
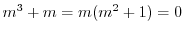 より特性根
より特性根
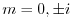 を得る.よって余関数は
を得る.よって余関数は
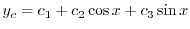
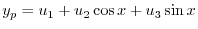
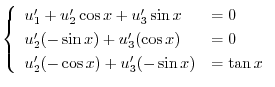
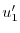 |
 |
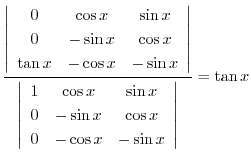 |
|
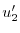 |
 |
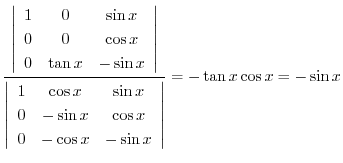 |
|
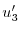 |
 |
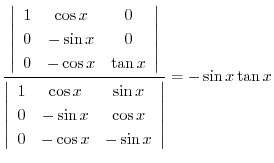 |
これより
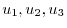 を求めると,
を求めると,
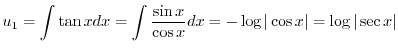
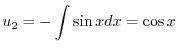
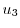 |
 |
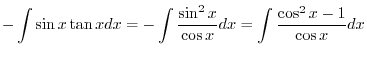 |
|
 |
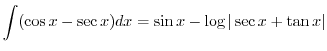 |
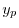 |
 |
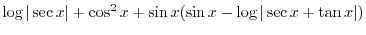 |
|
 |
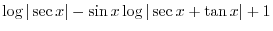 |
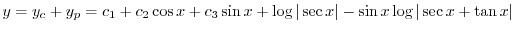

補助方程式
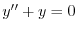 の特性方程式は
の特性方程式は
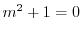 より特性根
より特性根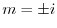 を得る.よって余関数は
を得る.よって余関数は
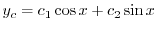
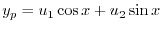
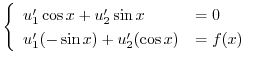
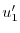 |
 |
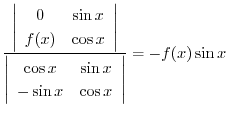 |
|
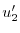 |
 |
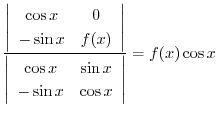 |
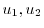 を求めると,
を求めると,
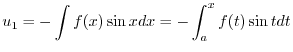
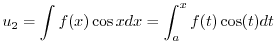
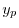 |
 |
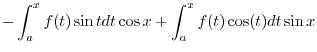 |
|
 |
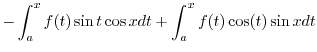 |
||
 |
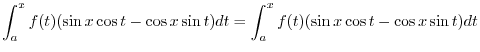 |
||
 |
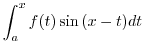 |