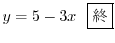Next: 2.4 解答 Up: 演習問題解答 Previous: 2.2 解答 索引
2.3
1.
(a)
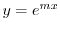 を解とおくと,特性方程式
を解とおくと,特性方程式
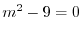 を得る.これより特性根は
を得る.これより特性根は
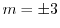 .よって基本解は
.よって基本解は
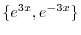

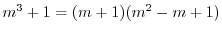
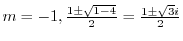 .よって基本解は
.よって基本解は
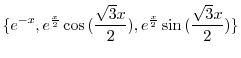

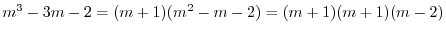
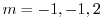 .よって基本解は
.よって基本解は
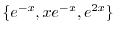

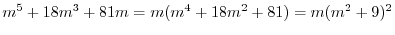
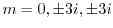 .よって基本解は
.よって基本解は
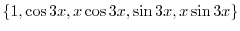

2.
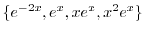
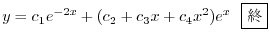
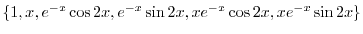
![$\displaystyle y = c_{1} + c_{2}x + e^{-x}[(c_{3} + c_{4})\cos{2x} + (c_{5} + c_{6}x)\sin{2x}] \ \ \framebox{終} $](img1021.png)
3.
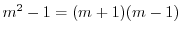
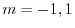 .よって基本解は
.よって基本解は
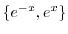
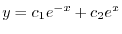
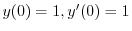 より
より
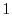 |
 |
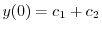 |
|
 |
 |
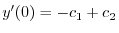 |
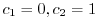 .よって
.よって
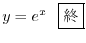
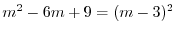
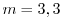 .よって基本解は
.よって基本解は
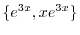
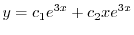
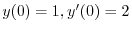 より
より
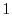 |
 |
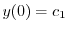 |
|
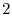 |
 |
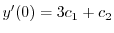 |
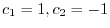 .よって
.よって
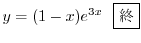
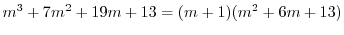
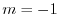 と
と
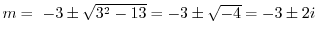 .よって基本解は
.よって基本解は
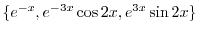
![$\displaystyle y = c_{1}e^{-x} + e^{-3x}[c_{2}\cos{2x} + c_{3}\sin{2x}] $](img1049.png)
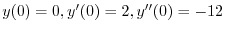 と
と
 |
 |
![$\displaystyle -c_{1}e^{-x} -3e^{-3x}[c_{2}\cos{2x} + c_{3}\sin{2x}]$](img1051.png) |
|
 |
![$\displaystyle e^{-3x}[-2c_{2}\sin{2x} + 2c_{3}\cos{2x}]$](img1052.png) |
||
 |
 |
![$\displaystyle c_{1}e^{-x} + 9e^{-3x}[c_{2}\cos{2x} + c_{3}\sin{2x}]$](img1054.png) |
|
 |
![$\displaystyle 6e^{-3x}[-2c_{2}\sin{2x} + 2c_{3}\cos{2x}] + e^{-3x}[-4c_{2}\cos{2x} - 4c_{3}\sin{2x}]$](img1055.png) |
| 0 |  |
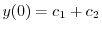 |
(A.1) |
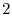 |
 |
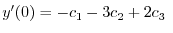 |
(A.2) |
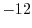 |
 |
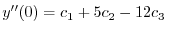 |
(A.3) |
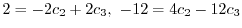 より
より
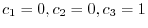 .
よって
.
よって
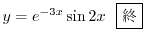
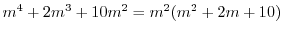
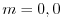 と
と
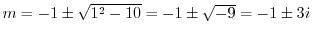 .よって基本解は
.よって基本解は
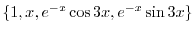
![$\displaystyle y = c_{1} + c_{2}x + e^{-x}[c_{3}\cos{3x} + c_{4}\sin{3x}] $](img1067.png)
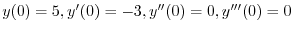 と
と
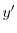 |
 |
![$\displaystyle c_{2} - e^{-x}[c_{3}\cos{3x} + c_{4}\sin{3x}]$](img1069.png) |
|
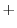 |
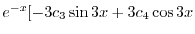 |
||
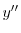 |
 |
![$\displaystyle e^{-x}[c_{3}\cos{3x} + c_{4}\sin{3x}]$](img1071.png) |
|
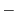 |
![$\displaystyle 2e^{-x}[-3c_{3}\sin{3x} + 3c_{4}\cos{3x}] + e^{-x}[-9c_{3}\cos{3x} - 9c_{4}\sin{3x}]$](img1072.png) |
||
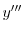 |
 |
![$\displaystyle - e^{-x}[c_{3}\cos{3x} + c_{4}\sin{3x}] + 3e^{-x}[-3c_{3}\sin{3x} + 3c_{4}\cos{3x}]$](img1074.png) |
|
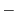 |
![$\displaystyle 3e^{-x}[-9c_{3}\cos{3x} - 9c_{4}\sin{3x}] + e^{-x}[27c_{3}\sin{3x} -27c_{4}\cos{3x}]$](img1075.png) |
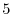 |
 |
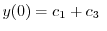 |
(A.4) |
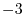 |
 |
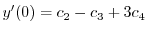 |
(A.5) |
| 0 |  |
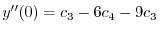 |
(A.6) |
| 0 |  |
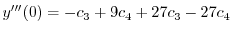 |
(A.7) |
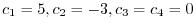 .よって
.よって