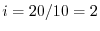Next: 1.7 解答 Up: 演習問題解答 Previous: 1.5 解答 索引
1.6
1.
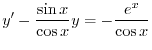
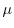 は
は
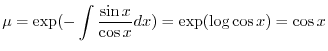
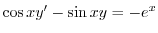
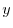 の導関数なので
の導関数なので
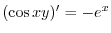
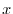 で積分すると
で積分すると
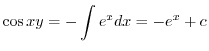
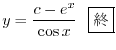
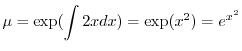
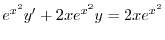
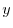 の導関数なので
の導関数なので
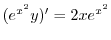
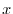 で積分すると
で積分すると
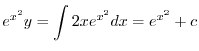
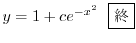
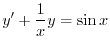
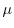 は
は
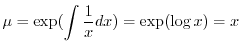
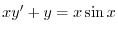
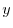 の導関数なので
の導関数なので
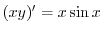
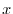 で積分すると
で積分すると
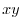 |
 |
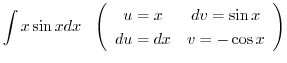 |
|
 |
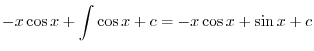 |
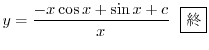
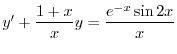
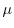 は
は
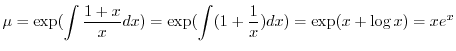
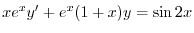
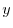 の導関数なので
の導関数なので
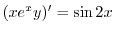
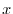 で積分すると
で積分すると
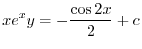
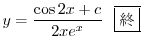
2.
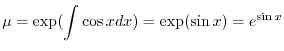
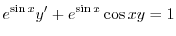
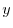 の導関数なので
の導関数なので
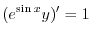
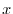 で積分すると
で積分すると
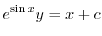
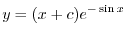
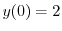 を用いると
を用いると
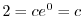 より
より
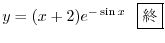
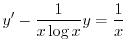
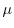 は
は
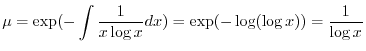
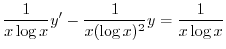
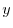 の導関数なので
の導関数なので
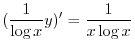
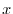 で積分すると
で積分すると
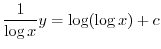
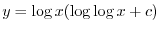
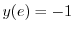 を用いると
を用いると
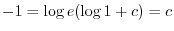 より
より
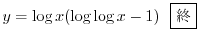
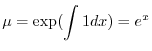
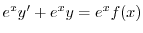
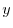 の導関数なので
の導関数なので
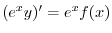
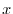 で積分すると
で積分すると
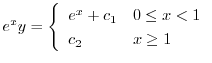
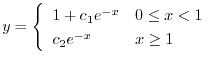
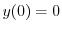 を用いると
を用いると
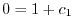 より
より
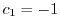 .よって
.よって
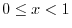 のとき,
のとき,
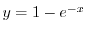 .また微分方程式の解は連続であると仮定できるので
.また微分方程式の解は連続であると仮定できるので
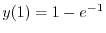 より
より
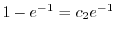 .よって
.よって
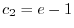 .これより
.これより
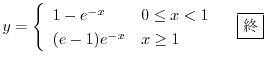
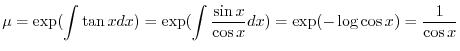
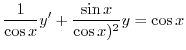
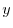 の導関数なので
の導関数なので
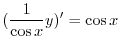
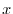 で積分すると
で積分すると
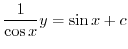
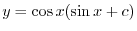
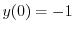 を用いると
を用いると
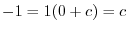 より
より
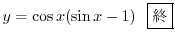
RL回路を流れる電流を表わす方程式は
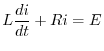
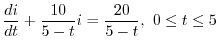
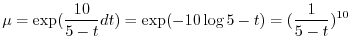
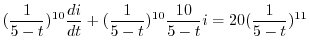
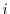 の導関数なので
の導関数なので
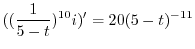
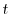 で積分すると
で積分すると
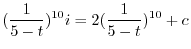
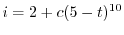
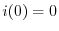 を用いると
を用いると
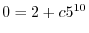 より
より
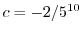 .よって
.よって
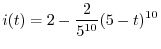
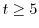 の場合を考えると,
の場合を考えると,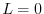 よりRL回路を流れる電流を表わす方程式は
よりRL回路を流れる電流を表わす方程式は
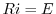 となり,
となり,