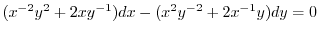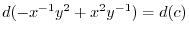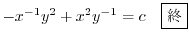Next: 1.6 解答 Up: 演習問題解答 Previous: 1.4 解答 索引
1.5
1.
(a)
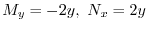 より完全微分形ではない.そこで積分因子を捜す.
より完全微分形ではない.そこで積分因子を捜す.
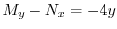 より
より
![$(1/N)[M_{y} - N_{x}]$](img598.png) を計算すると
を計算すると
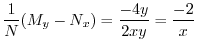
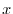 だけの関数なので積分因子は
だけの関数なので積分因子は
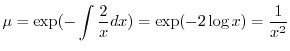
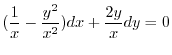
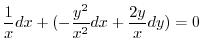
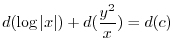
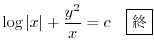
(b)
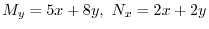 より完全微分形ではない.そこで積分因子を捜す.
より完全微分形ではない.そこで積分因子を捜す.
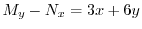 より
より
![$(1/N)[M_{y} - N_{x}]$](img598.png) を計算すると
を計算すると
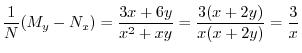
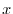 だけの関数なので積分因子は
だけの関数なので積分因子は
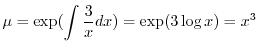
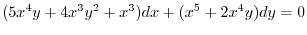
![$\displaystyle x^3 dx + [(5x^4 y + 4x^3 y^2) dx + (x^5 + 2x^4 y ) dy] = 0 $](img611.png)
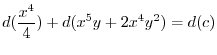
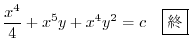
(c)
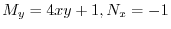 より完全微分形ではない.そこで積分因子を捜す.
より完全微分形ではない.そこで積分因子を捜す.
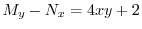 より
より
![$(1/M)[M_{y} - N_{x}]$](img616.png) を計算すると
を計算すると
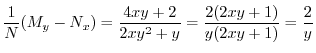
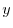 だけの関数なので積分因子は
だけの関数なので積分因子は
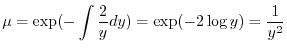
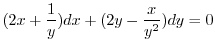
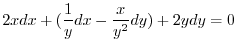
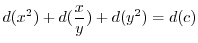
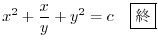
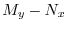 |
 |
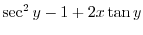 |
|
 |
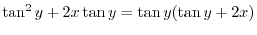 |
![$(1/M)[M_{y} - N_{x}]$](img616.png) を計算すると
を計算すると
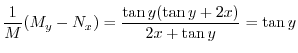
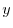 だけの関数なので積分因子は
だけの関数なので積分因子は
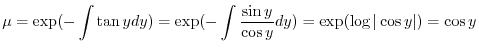
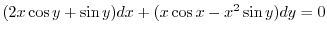
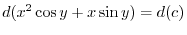
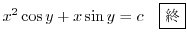
2.
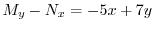
![$(1/N)[M_{y} - N_{x}], (1/M)[M_{y} - N_{x}]$](img634.png) は
は だけの関数にはならない.そこで積分因子を
だけの関数にはならない.そこで積分因子を
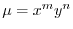 とおき,
とおき,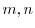 を求める.
を求める.
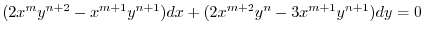
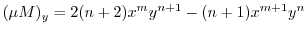
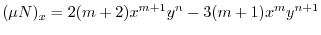
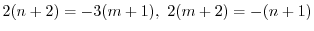
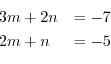
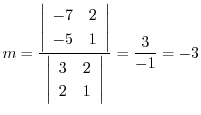
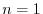 .これより
.これより
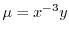 となる.これをもとの微分方程式にかけると
となる.これをもとの微分方程式にかけると
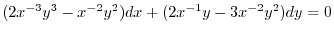
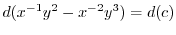
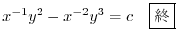
(b)
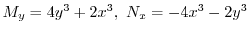 より完全微分形ではない.そこで積分因子を捜す.
より完全微分形ではない.そこで積分因子を捜す.
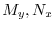 の形から積分因子を
の形から積分因子を
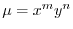 とおき,
とおき,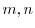 を求める.
を求める.
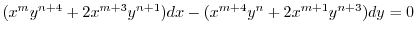
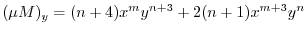
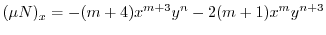
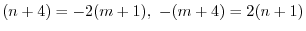
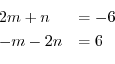
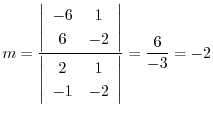
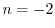 .これより
.これより
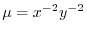 となる.これをもとの微分方程式にかけると
となる.これをもとの微分方程式にかけると