Next: 1.5 解答 Up: 演習問題解答 Previous: 1.3 解答 索引
1.4
1.
(a)
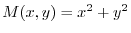 より
より
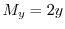 .また
.また
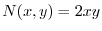 より
より
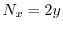 .よって
.よって
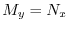 となり完全微分形.ここでくくり直しをおこなうと
となり完全微分形.ここでくくり直しをおこなうと
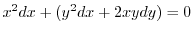
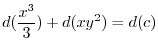
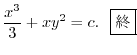
(b)
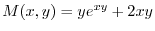 より
より
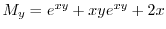 .また
.また
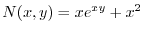 より
より
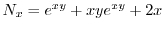 .よって
.よって
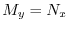 となり完全微分形.ここで
となり完全微分形.ここで
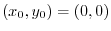 とおくと
とおくと
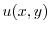 |
 |
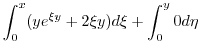 |
|
 |
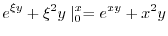 |
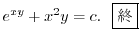
(c)
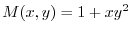 より
より
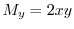 .また
.また
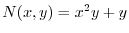 より
より
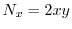 .よって
.よって
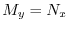 となり完全微分形.ここでくくり直しをおこなうと
となり完全微分形.ここでくくり直しをおこなうと
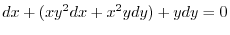
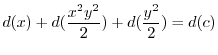
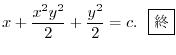
(d)
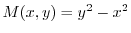 より
より
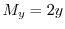 .また
.また
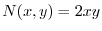 より
より
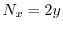 .よって
.よって
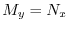 となり完全微分形.ここでくくり直しをおこなうと
となり完全微分形.ここでくくり直しをおこなうと
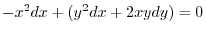
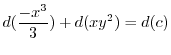
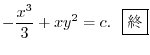
2.
(a)
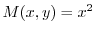 より
より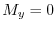 .また
.また
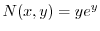 より
より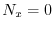 .よって
.よって
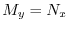 となり完全微分形.ここでくくり直しをおこなうと
となり完全微分形.ここでくくり直しをおこなうと
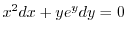
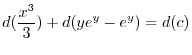
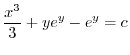
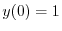 を用いると
を用いると
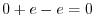 より
より
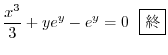
別解
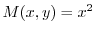 より
より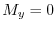 .また
.また
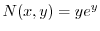 より
より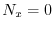 .よって
.よって
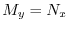 となり完全微分形.ここで
となり完全微分形.ここで
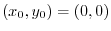 を用いると
を用いると
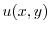 |
 |
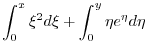 |
|
 |
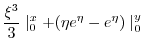 |
||
 |
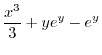 |
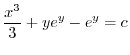
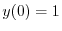 を用いると
を用いると
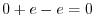 より
より
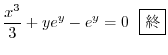
(b)
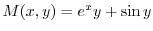 より
より
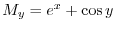 .また
.また
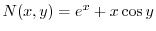 より
より
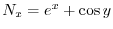 .よって
.よって
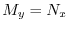 となり完全微分形.ここで
となり完全微分形.ここで
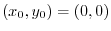 を用いると
を用いると
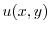 |
 |
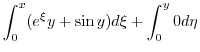 |
|
 |
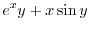 |
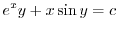
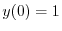 を用いると
を用いると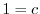 より
より
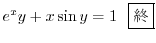
(c)
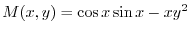 より
より
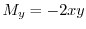 .また
.また
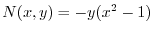 より
より
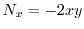 .よって
.よって
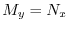 となり完全微分形.ここでくくり直しを行なうと
となり完全微分形.ここでくくり直しを行なうと
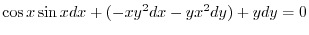
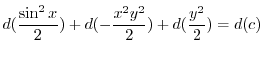
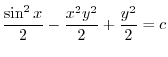
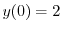 を用いると
を用いると
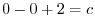 より
より