Next: 1.4 解答 Up: 演習問題解答 Previous: 1.2 解答 索引
1.3
1.
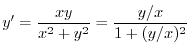
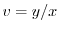 とおくと
とおくと
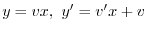 より
より
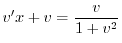
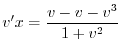
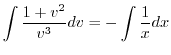
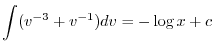
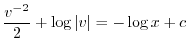
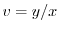 を代入すると
を代入すると
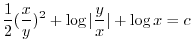
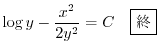
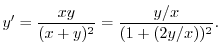
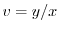 とおくと
とおくと
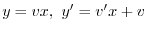 より
より
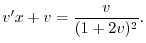
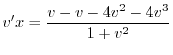
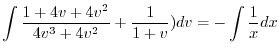
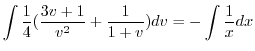
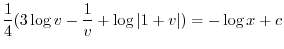
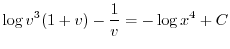
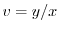 を代入すると
を代入すると
![$\displaystyle \log{[(\frac{y}{x})^{3} + (\frac{y}{x})^{4}]} - \frac{x}{y} = - \log{x^{4}} + C $](img460.png)
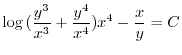
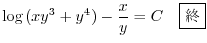
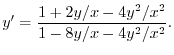
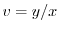 とおくと
とおくと
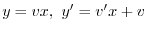 より
より
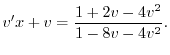
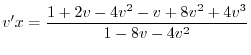
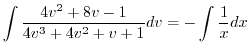
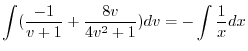
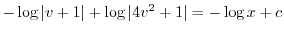
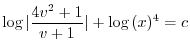
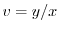 を代入すると
を代入すると
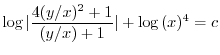
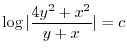
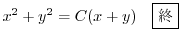
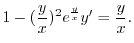
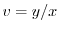 とおくと
とおくと
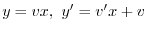 より
より
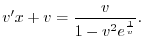
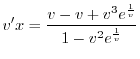
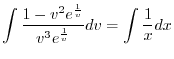
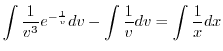
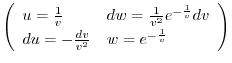
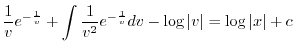
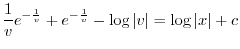
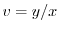 を代入すると
を代入すると
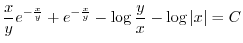
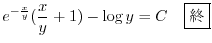
(e)
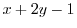 と
と
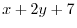 は同次関数ではないが,共に
は同次関数ではないが,共に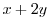 を含んでいるので,
を含んでいるので,
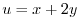 とおくと,
とおくと,
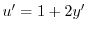 より
より
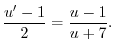
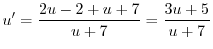
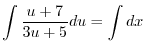
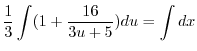
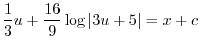
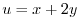 を代入すると
を代入すると
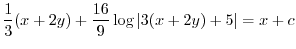
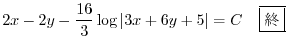
(f)
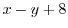 と
と
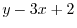 は同次関数ではないが,定数項がおちれば1次の同次関数になる.そこで
は同次関数ではないが,定数項がおちれば1次の同次関数になる.そこで
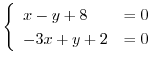
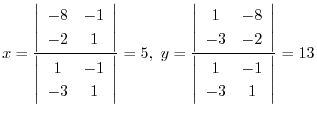
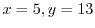 が原点になるように座標軸の移動を行なうと,
が原点になるように座標軸の移動を行なうと,
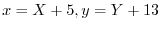 より
より
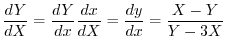
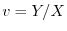 とおくと,
とおくと,
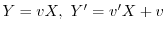 より
より
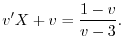
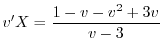
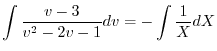
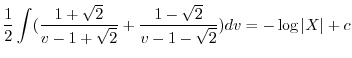
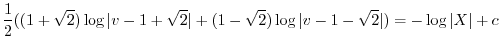
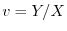 を代入すると
を代入すると
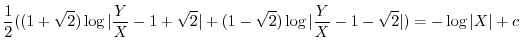
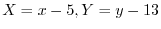 で置き換えると
で置き換えると
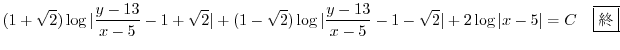
2.
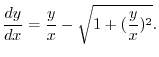
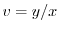 とおくと,
とおくと,
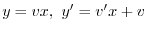 より
より
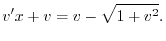
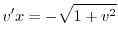
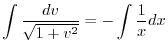
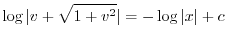
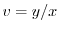 を代入すると
を代入すると
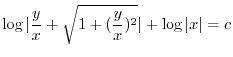
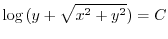
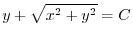
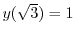 より
より
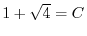 .よって
.よって
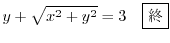
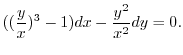
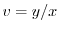 とおくと,
とおくと,
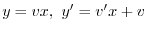 より
より
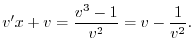
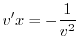
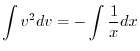
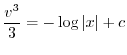
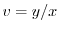 を代入すると
を代入すると
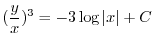
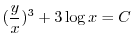
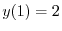 より
より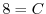 .よって
.よって
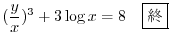
例題1.8は座標軸の移動を行なって定数項を落とすことができた.残念ながら例題1.9は
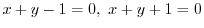 と2つの平行な直線を扱っているため,座標軸の移動では定数項を落とすことができない.
と2つの平行な直線を扱っているため,座標軸の移動では定数項を落とすことができない.
