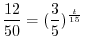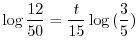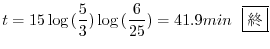Next: 1.3 解答 Up: 演習問題解答 Previous: 1.1 解答 索引
1.2
1.
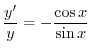
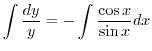
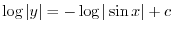
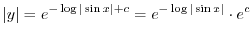
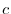 は任意の定数より
は任意の定数より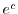 を
を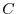 を用いて表わす.
これより
を用いて表わす.
これより
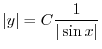
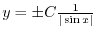 となるが
となるが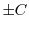 はまた定数なので
はまた定数なので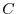 を用いて表わすと
を用いて表わすと
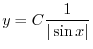
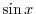 の絶対値をはずすと
の絶対値をはずすと
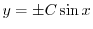 となるが
となるが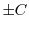 はまた定数なので
はまた定数なので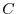 を用いて表わすと
を用いて表わすと
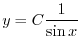
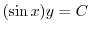
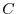 を用いて異なる値を表わすことを
を用いて異なる値を表わすことを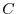 の乱用という.これより
の乱用という.これより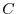 の乱用を黙って用いる.
の乱用を黙って用いる.

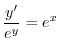
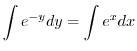
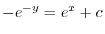
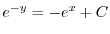
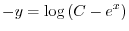
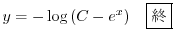
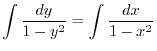
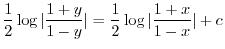
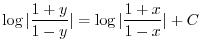
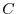 の乱用を行なうと
の乱用を行なうと
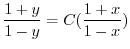
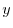 について解くと
について解くと
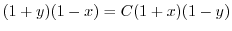
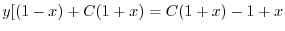
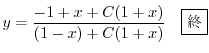
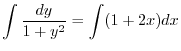
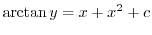
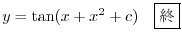
2.
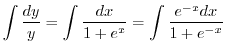
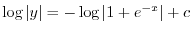
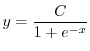
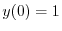 を用いると
を用いると
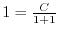 より
より
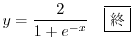
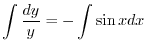
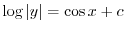
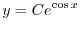
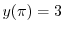 を用いると
を用いると
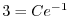 より
より
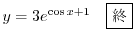
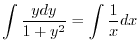
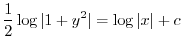
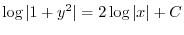
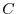 の乱用を行なうと
の乱用を行なうと
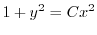
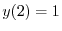 を用いると
を用いると
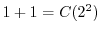 より
より
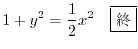
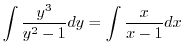
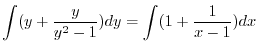
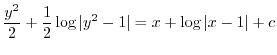
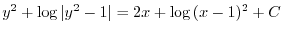
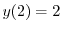 を用いると
を用いると
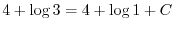 より
より
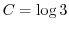 .
よって
.
よって
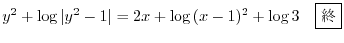
3.
(a) Newtonの冷却の法則を用いてこの問題を定式化すると
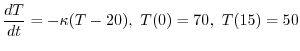
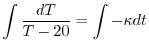
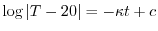
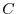 の乱用を行なうと
の乱用を行なうと
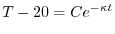
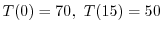 を用いると
を用いると
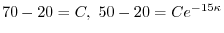 より
より
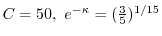 .これより
.これより
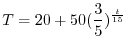
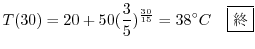
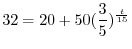
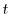 について解くと
について解くと