Next: 1.2 解答 Up: 演習問題解答 Previous: 演習問題解答 索引
1.1
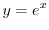 より
より
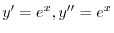 .よって
.よって
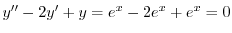
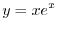 より
より
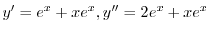 .よって
.よって
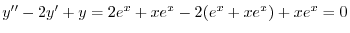
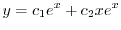 より
より
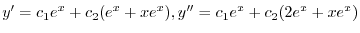 .よって
.よって
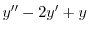 |
 |
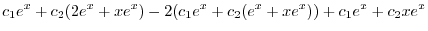 |
|
 |
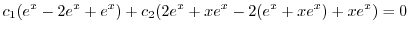 |
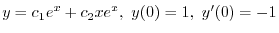 のとき
のとき
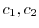 を求める.まず,
を求める.まず, 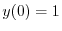 より
より
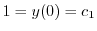 .よって
.よって 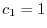 .次に,
.次に,
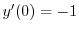 より
より
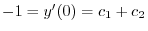 .よって
.よって
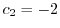 .
.

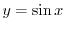 より
より
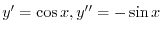 .よって
.よって
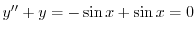
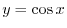 より
より
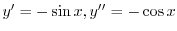 .よって
.よって
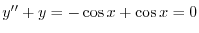
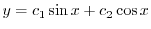 より
より
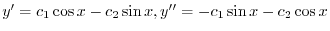 .よって
.よって
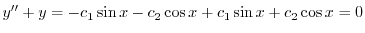
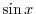 と
と 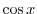 で張られるベクトル空間について考える.まず,
で張られるベクトル空間について考える.まず,
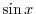 と
と 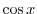 で張られるベクトル空間は次のように表わせる.
で張られるベクトル空間は次のように表わせる.
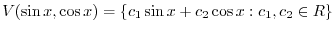
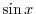 と
と 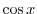 の一次結合全体の集まりとなる.また,このベクトル空間の次元を求めると,
の一次結合全体の集まりとなる.また,このベクトル空間の次元を求めると,
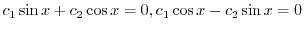
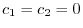 となる.つまり
となる.つまり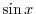 と
と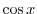 は一次独立だといえる.よって,
は一次独立だといえる.よって,
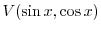 の次元 は2である.
の次元 は2である.
