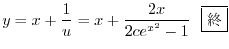Next: 1.8 解答 Up: 演習問題解答 Previous: 1.6 解答 索引
1.7
1.
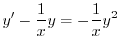
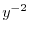 をかけて整理すると
をかけて整理すると
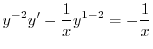
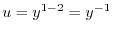 とおくと
とおくと
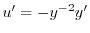 より
より
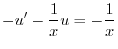
 について線形なので,
について線形なので, についての標準形に直すと
についての標準形に直すと
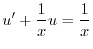
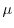 を求めると
を求めると
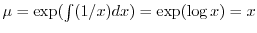 となる.これを
となる.これを についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
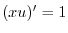
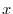 について積分すると
について積分すると
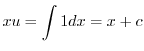
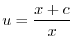
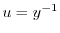 を代入すると
を代入すると
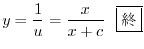
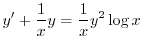
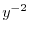 をかけて整理すると
をかけて整理すると
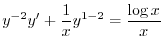
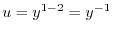 とおくと
とおくと
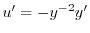 より
より
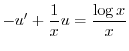
 について線形なので,
について線形なので, についての標準形に直すと
についての標準形に直すと
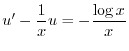
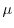 を求めると
を求めると
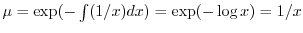 となる.これを
となる.これを についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
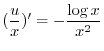
 について積分すると
について積分すると
 |
 |
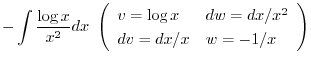 |
|
 |
![$\displaystyle - [- \frac{\log{x}}{x} - \int \frac{-1}{x^2} dx ] = \frac{\log{x}}{x} + \frac{1}{x} + c$](img763.png) |
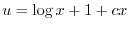 となり
となり
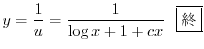
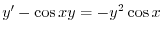
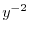 をかけて整理すると
をかけて整理すると
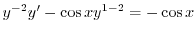
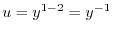 とおくと
とおくと
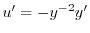 より
より
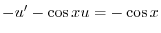
 について線形なので,
について線形なので, についての標準形に直すと
についての標準形に直すと
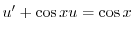
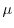 を求めると
を求めると
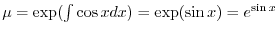 となる.これを
となる.これを についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
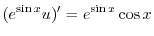
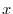 について積分すると
について積分すると
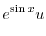 |
 |
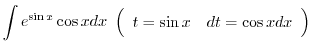 |
|
 |
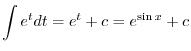 |
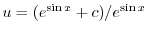 となり
となり
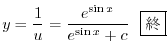
2.
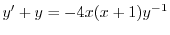
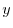 をかけて整理すると
をかけて整理すると
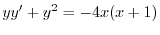
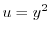 とおくと
とおくと
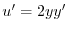 より
より
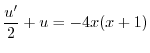
 について線形なので,
について線形なので, についての標準形に直すと
についての標準形に直すと
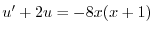
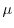 を求めると
を求めると
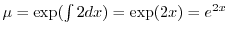 となる.これを
となる.これを についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
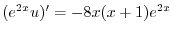
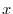 について積分すると
について積分すると
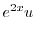 |
 |
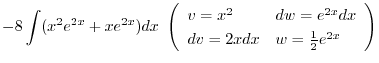 |
|
 |
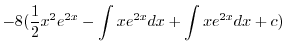 |
||
 |
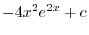 |
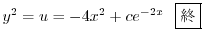
(b)
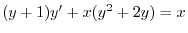 において,
において,
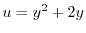 とおくと
とおくと
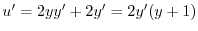 となる.これらを元の微分方程式に代入すると
となる.これらを元の微分方程式に代入すると
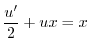
 について線形なので,
について線形なので, についての標準形に直すと
についての標準形に直すと
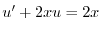
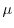 を求めると
を求めると
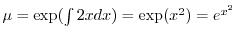 となる.これを
となる.これを についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
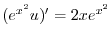
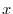 について積分すると
について積分すると
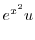 |
 |
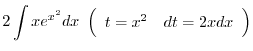 |
|
 |
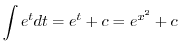 |
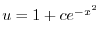 となり
となり
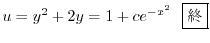
3.
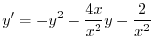
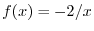 はこの方程式のひとつの解であるから
はこの方程式のひとつの解であるから
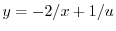 とおくと
とおくと
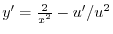 .これらを標準形に代入すると
.これらを標準形に代入すると
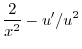 |
 |
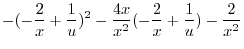 |
|
 |
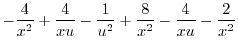 |
||
 |
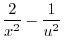 |
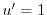 .よって
.よって
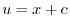
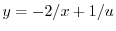 より
より
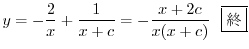
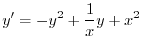
 はこの方程式のひとつの解となるので
はこの方程式のひとつの解となるので
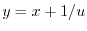 とおくと
とおくと
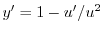 .これらを標準形に代入すると
.これらを標準形に代入すると
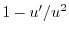 |
 |
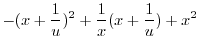 |
|
 |
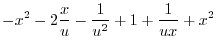 |
||
 |
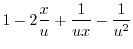 |
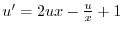 .これは
.これは について一階線形なので標準形に書き直すと
について一階線形なので標準形に書き直すと
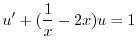
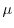 を求めると
を求めると
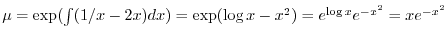 となる.これを
となる.これを についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
についての標準形にかけると,左辺は必ず積分因子かける従属変数の導関数になるので
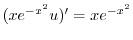
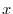 について積分すると
について積分すると
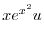 |
 |
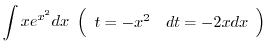 |
|
 |
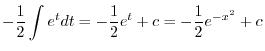 |
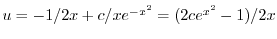 となる.よって
となる.よって