Next: 8.1 解答 Up: 演習問題解答 Previous: 7.3.2 索引
7.3.3
この問題の数学的モデルは
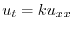
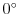 より
より
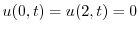 .また定常温度分布が
.また定常温度分布が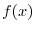 より
より
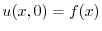 .よって次のような境界値問題を得る.
.よって次のような境界値問題を得る.
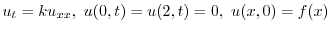
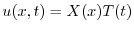 とおき,一次元熱伝導方程式に代入すると
とおき,一次元熱伝導方程式に代入すると
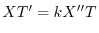
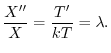
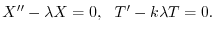
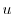 の境界条件を用いると,すべての
の境界条件を用いると,すべての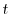 に対して
に対して
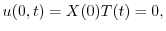
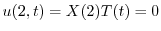
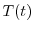 が0でないならば,
が0でないならば,
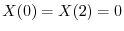 を意味する.よってこれよりSturm-Liouville問題
を意味する.よってこれよりSturm-Liouville問題
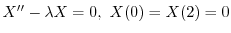
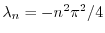 ,固有関数
,固有関数
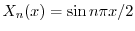 をもっている.また,固有値
をもっている.また,固有値
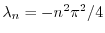 のとき,
のとき,
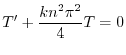
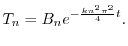
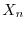 と
と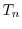 の積
の積
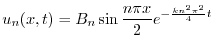
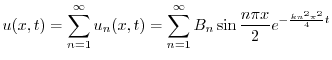
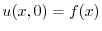 より
より
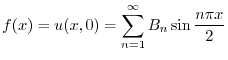
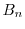 |
 |
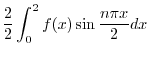 |
|
 |
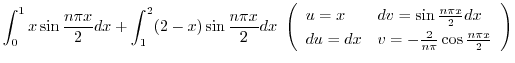 |
||
 |
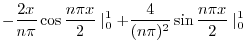 |
||
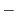 |
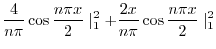 |
||
 |
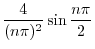 |
||
 |
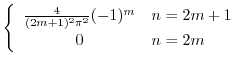 |
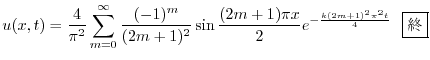
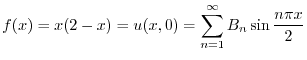
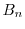 |
 |
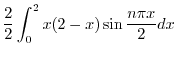 |
|
 |
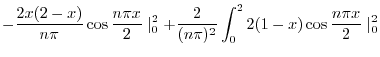 |
||
 |
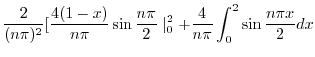 |
||
 |
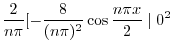 |
||
 |
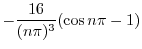 |
||
 |
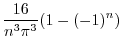 |
||
 |
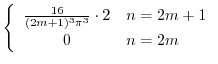 |
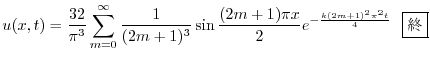
3.  を棒の温度とすると,定常温度分布は
を棒の温度とすると,定常温度分布は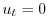 を満たす.つまりラプラス方程式
を満たす.つまりラプラス方程式
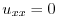 を満たす.よって棒の温度は
を満たす.よって棒の温度は
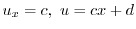
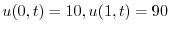 より
より
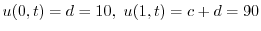
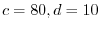 .これより
.これより
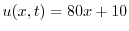 .
.

4.
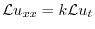
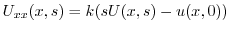
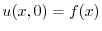 より
より
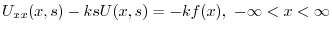
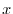 についての2階の線形微分方程式であるから,定数変化法を用いて解くことができる.
についての2階の線形微分方程式であるから,定数変化法を用いて解くことができる.
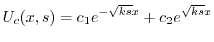
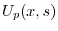 を定数変化法で求める.
を定数変化法で求める.
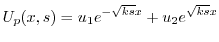
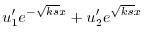 |
 |
0 | |
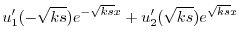 |
 |
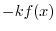 |
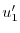 |
 |
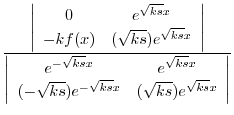 |
|
 |
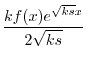 |
||
 |
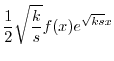 |
||
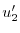 |
 |
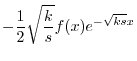 |
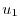 |
 |
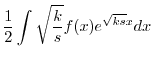 |
|
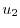 |
 |
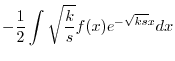 |
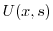 |
 |
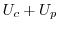 |
|
 |
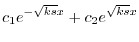 |
||
 |
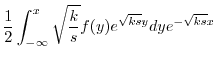 |
||
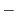 |
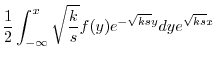 |
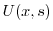 は
は
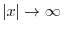 で有界であるから
で有界であるから
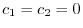 .よって
.よって
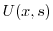 |
 |
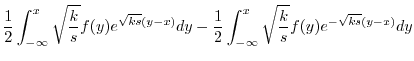 |
|
 |
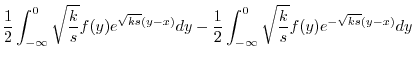 |
||
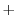 |
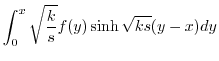 |
||
 |
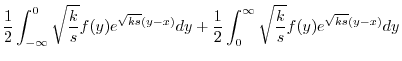 |
||
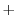 |
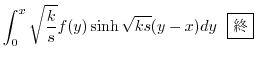 |