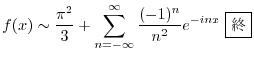Next: 6.4 解答 Up: 演習問題解答 Previous: 6.2 解答 索引
6.3
1.
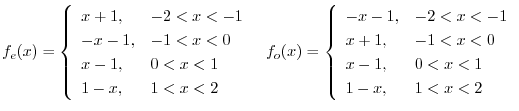
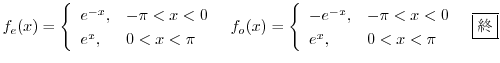
2.
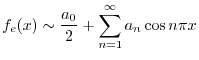
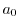 |
 |
 |
|
 |
 |
 |
|
 |
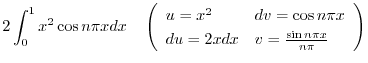 |
||
 |
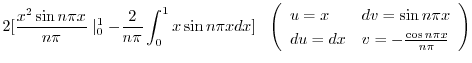 |
||
 |
![$\displaystyle 2[\frac{\sin{n\pi}}{n\pi} - \frac{2}{n\pi}(-\frac{x\cos{n\pi x}}{n\pi}\mid_{0}^{1} + \frac{1}{n\pi}\int_{0}^{1}\cos{n\pi x}dx)]$](img2350.png) |
||
 |
 |
||
 |
 |
||
 |
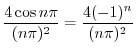 |
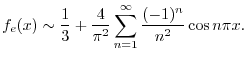
![\includegraphics[width=10cm]{DFQ/Fig6.3-2(a)1.eps}](img2413.png)
次に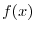 のフーリエ正弦級数を求める.
のフーリエ正弦級数を求める.
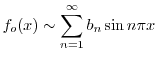
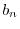 |
 |
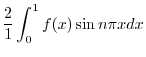 |
|
 |
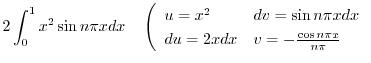 |
||
 |
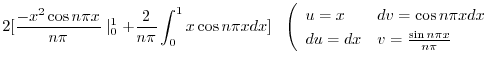 |
||
 |
![$\displaystyle 2[\frac{-\cos{n\pi}}{n\pi} + \frac{2}{n\pi}(\frac{x\sin{n\pi x}}{n\pi}\mid_{0}^{1} - \frac{1}{n\pi}\int_{0}^{1}\sin{n\pi x}dx)]$](img2359.png) |
||
 |
![$\displaystyle 2[\frac{-\cos{n\pi}}{n\pi} + \frac{2}{n\pi}(\frac{\sin{n\pi }}{n\pi}+ \frac{\cos{n\pi x}}{(n\pi)^2}\mid_{0}^{1})]$](img2360.png) |
||
 |
![$\displaystyle 2[\frac{-\cos{n\pi}}{n\pi} + \frac{2}{n\pi}( \frac{\cos{n\pi} - 1}{(n\pi)^2})]$](img2361.png) |
||
 |
![$\displaystyle 2[\frac{-(-1)^n}{n\pi} + \frac{2((-1)^n - 1)}{(n\pi)^3}]$](img2362.png) |
![$\displaystyle f_{o}(x) \sim 2\sum_{n=1}^{\infty}[\frac{(-1)^{n+1}}{n\pi} + \frac{2((-1)^{n} - 1)}{(n\pi)^3}]\sin{n\pi x} $](img2363.png)
![\includegraphics[width=10cm]{DFQ/Fig6.3-2(a)2.eps}](img2414.png)

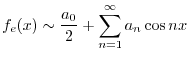
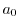 |
 |
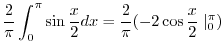 |
|
 |
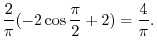 |
||
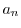 |
 |
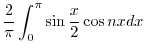 |
|
 |
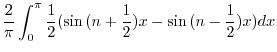 |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{-\cos{(n+\frac{1}{2})x}}{n + \frac{1}{2}} + \frac{\cos{(n-\frac{1}{2})x}}{n - \frac{1}{2}}\mid_{0}^{\pi}]$](img2369.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{-\cos{(n+\frac{1}{2})\pi + 1}}{n + \frac{1}{2}} + \frac{\cos{(n-\frac{1}{2})\pi - 1}}{n - \frac{1}{2}}]$](img2370.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{\sin{n\pi} + 1}{n + \frac{1}{2}} + \frac{-\sin{n\pi } - 1}{n - \frac{1}{2}}]$](img2371.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{-1}{n^2 - \frac{1}{4}}] = \frac{4}{\pi}[\frac{-1}{4n^2 - 1}]$](img2372.png) |
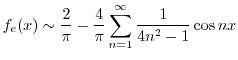
![\includegraphics[width=10cm]{DFQ/Fig6.3-2(b)1.eps}](img2415.png)
次に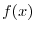 のフーリエ正弦級数を求める.
のフーリエ正弦級数を求める.
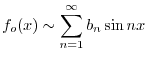
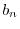 |
 |
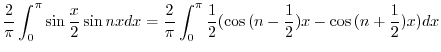 |
|
 |
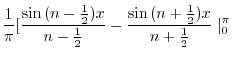 |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{\sin{(n-\frac{1}{2})\pi }}{n - \frac{1}{2}} - \frac{\sin{(n+ \frac{1}{2})\pi}}{n + \frac{1}{2}}]$](img2377.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{-\cos{n\pi} }{n - \frac{1}{2}} - \frac{\cos{n\pi } }{n + \frac{1}{2}} ]$](img2378.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{-2n\cos{n\pi}}{n^2 - \frac{1}{4} } ]$](img2379.png) |
||
 |
![$\displaystyle \frac{8}{\pi}[\frac{n(-1)^{n+1}}{4n^2 - 1}]$](img2380.png) |
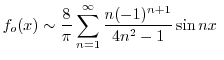
![\includegraphics[width=10cm]{DFQ/Fig6.3-2(b)2.eps}](img2416.png)

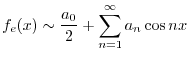
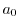 |
 |
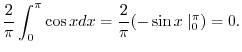 |
|
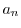 |
 |
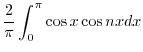 |
|
 |
 |
||
 |
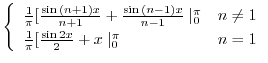 |
||
 |
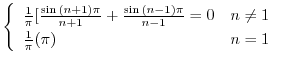 |
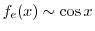
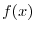 のフーリエ正弦級数を求める.
のフーリエ正弦級数を求める.
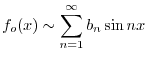
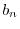 |
 |
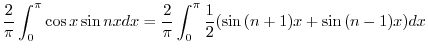 |
|
 |
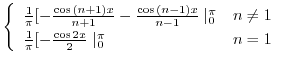 |
||
 |
![$\displaystyle \left\{\begin{array}{ll}
\frac{1}{\pi}[-\frac{\cos{(n+1)\pi + 1}}...
...rac{1}{\pi}[-\frac{\cos{2\pi}}{2} + \frac{1}{2}] & \ \ n = 1
\end{array}\right.$](img2390.png) |
||
 |
![$\displaystyle \left\{\begin{array}{cl}
\frac{1}{\pi}[-\frac{2n\cos{(n+1)\pi + 2n}}{n^2 - 1}] & \ \ n \neq 1\\
0& \ \ n = 1
\end{array}\right.$](img2391.png) |
||
 |
![$\displaystyle \frac{2}{\pi}[\frac{(1 - n(-1)^{n+1})}{n^2 - 1}] \ \ \ n \geq 2$](img2392.png) |
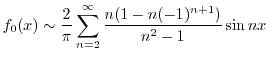
![\includegraphics[width=10cm]{DFQ/Fig6.3-2(a)2.eps}](img2414.png)

3.
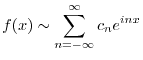
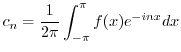
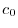 |
 |
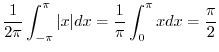 |
|
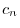 |
 |
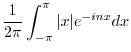 |
|
 |
![$\displaystyle \frac{1}{2\pi}[\int_{-\pi}^{\pi}\vert x\vert(\cos{nx} + i\sin{nx})dx ]$](img2399.png) |
||
 |
![$\displaystyle \frac{1}{2\pi}[\int_{-\pi}^{\pi}\vert x\vert\cos{nx}dx] = \frac{1}{\pi}\int_{0}^{\pi}x\cos{nx} dx ]$](img2400.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{x\sin{nx}}{n}\mid_{0}^{\pi} - \frac{1}{n} \int_{0}^{\infty}\sin{nx}dx]$](img2401.png) |
||
 |
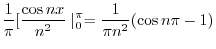 |
||
 |
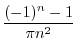 |
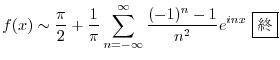
 |
 |
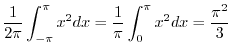 |
|
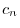 |
 |
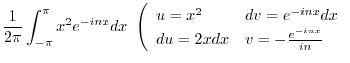 |
|
 |
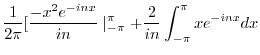 |
||
 |
![$\displaystyle \frac{1}{2\pi}[\frac{-\pi^{2}e^{-in\pi} + (-\pi)^{2}e^{in\pi}}{in...
...ac{-xe^{-inx}}{in}\mid_{-\pi}^{\pi} + \frac{1}{in}\int_{-\pi}^{\pi}e^{-inx}dx)]$](img2408.png) |
||
 |
![$\displaystyle \frac{1}{2\pi}[\frac{2(-\pi e^{-in\pi} -\pi e^{in\pi})}{(in)^{2}}...
...ac{1}{(in)^{3}}e^{-inx}\mid_{-\pi}^{\pi}] \ (e^{in\pi} = e^{-in\pi} = (-1)^{n})$](img2409.png) |
||
 |
![$\displaystyle \frac{1}{2\pi}[\frac{-4\pi (-1)^{n}}{(in)^{2}} - \frac{1}{(in)^{3}}(e^{-in\pi} - e^{in\pi})]$](img2410.png) |
||
 |
![$\displaystyle \frac{1}{2\pi}[\frac{-4\pi(-1)^{n}}{(in)^2} ]= \frac{(-1)^n}{n^2}$](img2411.png) |