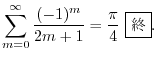Next: 6.3 解答 Up: 演習問題解答 Previous: 6.1 解答 索引
6.2
![$\displaystyle a_{0} = \frac{1}{\pi}[\int_{-\pi}^{0}1dx + \int_{0}^{\pi}2dx] = \frac{1}{\pi}[\pi + 2\pi] = 3 $](img2289.png)
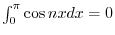 より
より
![$\displaystyle a_{n} = \frac{1}{\pi}[\int_{-\pi}^{0}\cos{nx}dx + \int_{0}^{\pi}2\cos{nx}dx] = 0 $](img2291.png)
 |
 |
![$\displaystyle \frac{1}{\pi}[\int_{-\pi}^{0}\sin{nx}dx + \int_{0}^{\pi}2\sin{nx}dx]$](img2293.png) |
|
 |
![$\displaystyle \frac{1}{\pi}[-\frac{\cos{nx}}{n}\mid_{-\pi}^{0} - \frac{2\cos{nx}}{n}\mid_{0}^{\pi}]$](img2294.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{-1 + \cos{n\pi}}{n} - \frac{2(\cos{n\pi} - 1)}{n}]$](img2295.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{1 - \cos{n\pi}}{n}] = \frac{1 - (-1)^{n}}{n\pi}$](img2296.png) |
 のフーリエ級数は
のフーリエ級数は
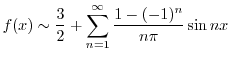
![\includegraphics[width=10cm]{DFQ/Fig6.2-1(a).eps}](img2339.png)

![$\displaystyle a_{0} = \frac{1}{\pi}\int_{-\pi}^{\pi}\vert\sin{x}\vert dx = \fra...
...int_{0}^{\pi}\sin{x}dx = \frac{2}{\pi}[-\cos{x}\mid_{0}^{\pi}] = \frac{4}{\pi} $](img2300.png)
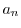 |
 |
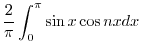 |
|
 |
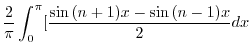 |
||
 |
![$\displaystyle \left\{\begin{array}{ll}
\frac{1}{\pi}[-\frac{\cos{(n+1)x}}{n+1} ...
...{\cos{(n-1)x}}{n-1} \mid_{0}^{\pi}] & (n \neq 1)\\
0 & n =1
\end{array}\right.$](img2304.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[-\frac{\cos{(n+1)\pi}}{n+1} +\frac{\cos{(n-1)\pi}}{n-1} + \frac{1}{n+1} - \frac{1}{n-1}]$](img2305.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[-\frac{(-1)^{n+1}}{n+1} +\frac{(-1)^{n-1}}{n-1} + \frac{-2}{n^2 - 1} ]$](img2306.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{n((-1)^{n-1} - (-1)^{n+1}) + (-1)^{n+1} + (-1)^{n-1} -2}{n^2 - 1} ]$](img2307.png) |
||
 |
![$\displaystyle \frac{1}{\pi}[\frac{2(-1)^{n+1} -2}{n^2 - 1} ]$](img2308.png) |
||
 |
![$\displaystyle \frac{2}{\pi}[\frac{(-1)^{n+1} -1}{n^2 - 1} ]$](img2309.png) |
||
 |
![$\displaystyle \frac{2}{\pi}[\frac{-2}{4m^2 - 1}] \ \ (n = 2m)$](img2310.png) |
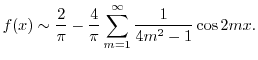
![\includegraphics[width=10cm]{DFQ/Fig6.2-1(b).eps}](img2340.png)

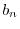 |
 |
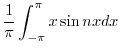 |
|
 |
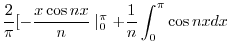 |
||
 |
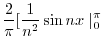 |
||
 |
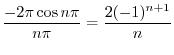 |
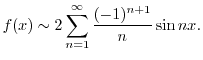
![\includegraphics[width=10cm]{DFQ/Fig6.2-1(c).eps}](img2341.png)

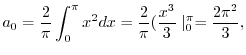
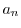 |
 |
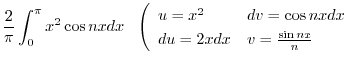 |
|
 |
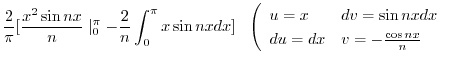 |
||
 |
![$\displaystyle \frac{-4}{n\pi}[\frac{-x \cos{nx}}{n}\mid_{0}^{\pi} + \frac{1}{n}\int_{0}^{\pi}\cos{nx}dx ]$](img2322.png) |
||
 |
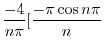 |
||
 |
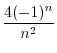 |
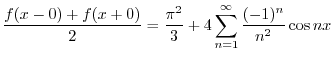
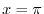 とおくと,
とおくと,
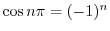 より
より
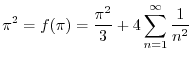
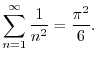
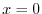 とおくと,
とおくと,
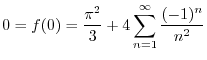
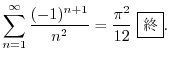
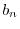 |
 |
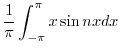 |
|
 |
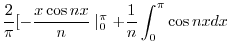 |
||
 |
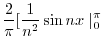 |
||
 |
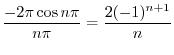 |
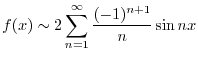
 はDirichlet条件を満たすので
はDirichlet条件を満たすので
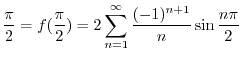
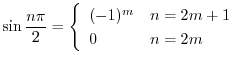
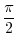 |
 |
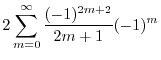 |
|
 |
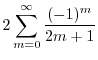 |