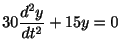: 演習問題
: 線形微分方程式
: 演習問題
目次
索引
微分して自分自身の定数倍になるのは指数関数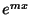 以外にありません.もう少し正確にいうと
以外にありません.もう少し正確にいうと
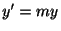 の完全解は
の完全解は
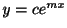 だということです.そこで
の解を捜すとき,その候補として
だということです.そこで
の解を捜すとき,その候補として
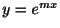 をあげます.そのとき
より
をあげます.そのとき
より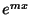 が微分方程式
が微分方程式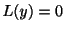 の解になるための必要十分条件は
となります.この多項式
の解になるための必要十分条件は
となります.この多項式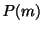 を特性多項式(characteristic polynomial)といい,
を特性多項式(characteristic polynomial)といい,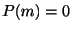 を特性方程式(characteristic equation)といいます.
を特性方程式(characteristic equation)といいます.
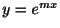 の変換により
の変換により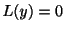 を解くという問題が,多項式
を解くという問題が,多項式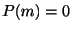 を解くという問題に簡素化されました.
を解くという問題に簡素化されました.
例題 2.7
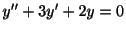
を解け.
解
特性方程式
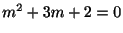 の根は
の根は
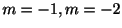 .よって
.よって
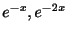 は解である.またこの2つの関数は例題2.2より一次独立.したがって一般解は
は解である.またこの2つの関数は例題2.2より一次独立.したがって一般解は
である.
例題 2.8
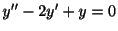
を解け.
解
特性方程式
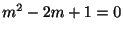 の根は
の根は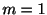 .よって
.よって
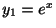 は解である.
この微分方程式は2階なので一般解を得るには一次独立な解がもうひとつ必要である.
演習問題2.2.1よりもうひとつの解
は解である.
この微分方程式は2階なので一般解を得るには一次独立な解がもうひとつ必要である.
演習問題2.2.1よりもうひとつの解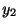 を求めると
を求めると
となる.よって一般解は
である.
この例題を一般化すると次の定理を得ます.
証明
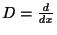 とおく.すると
とおく.すると
は
と表わせる.また
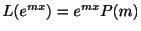 より,
より,
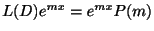 と表わせる.ここで
と表わせる.ここで
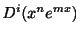 を計算すると,
となるので
したがって
を計算すると,
となるので
したがって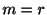 が
が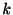 重根のとき
重根のとき
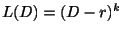 で
次に
で
次に
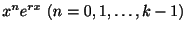 が一次独立であることを示す.
とおくと
よって
が一次独立であることを示す.
とおくと
よって
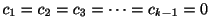 .
.
例題 2.9
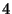
階の線形微分方程式
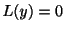
の特性方程式
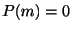
の根が
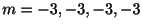
とする.このとき一般解を求めよ.
解
定理2.7より
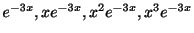 は
は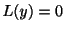 の一次独立な解である.よって一般解は
の一次独立な解である.よって一般解は
となる.
ここまでの例題の方程式の根はすべて実数でしたが,定理2.7は複素数の場合にも成り立ちます.ただ対応する解を複素指数関数を用いず,三角関数を用いて表わすことがよくあります.
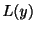 の係数を実数とします.
の係数を実数とします.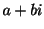 が対応する特性方程式
が対応する特性方程式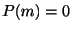 の特性根ならばその共役
の特性根ならばその共役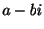 も特性根です.したがって
も特性根です.したがって
はともに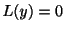 の解です.ここでEulerの公式(Euler's formula)
の解です.ここでEulerの公式(Euler's formula)
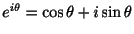 と解の線形性により
と解の線形性により
も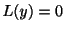 の解です.また
の解です.また
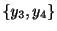 が一次独立であることは簡単に示せるでしょう.よって,特性方程式の複素数根の
が一次独立であることは簡単に示せるでしょう.よって,特性方程式の複素数根の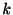 重根に対する基本解は,次のように表わせます.
重根に対する基本解は,次のように表わせます.
例題 2.10
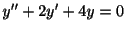
を解け.
解
特性方程式
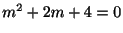 の根は
の根は
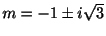 .よって
.よって
は基本解である.これより一般解は
で与えられる.ちなみに
も基本解である.
ここまでをまとめると,同次定数係数線形微分方程式の解はいつも
の一次結合で表わされるということです.
次の例題はNewtonの第2法則(Newton's second law)とHookeの法則(Hooke's Law)を用いて,一端を固定したバネにつり下げられた物体の運動の状態を調べるものです.そこで復習.
物体の質量を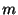 ,バネの弾力定数を
,バネの弾力定数を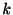 ,ダッシュポットの摩擦による減衰力は物体の速度
,ダッシュポットの摩擦による減衰力は物体の速度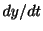 に比例するとき,この物体に働いている力は
に比例するとき,この物体に働いている力は
図 2.2:
バネの振動
![\begin{figure}\begin{center}
\includegraphics[width=5cm]{DFQ/Fig1-3.eps}
\end{center}\end{figure}](img658.gif) |
1. 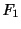 |
= 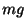 重力が物体に働く力 重力が物体に働く力 |
2. 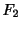 |
= 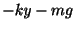 バネが元に戻ろうろとする力 バネが元に戻ろうろとする力 |
3. 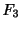 |
=
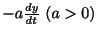 ダッシュポットの摩擦による減衰力 ダッシュポットの摩擦による減衰力 |
4. 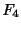 |
= 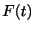 外部から物体に働いている力 外部から物体に働いている力 |
で与えられます.また垂直方向の力の差はNewtonの第2法則より,質量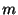 と加速度
と加速度
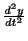 の積で表わされます.よって運動方程式
の積で表わされます.よって運動方程式
または
が導けます.
例題 2.11
上端を固定したばねの下端に質量
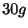
のおもりをつるすと,ばねは
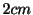
伸びて静止の状態になった.この状態からおもりを
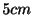
引き下げて手放すとき,そのおもりの運動の状態を調べよ.ただし重力は
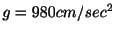
とし,空気抵抗はないものとする.
解
運動方程式は質量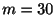 ,バネ定数
,バネ定数
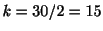 より
より
となる.これは2階の線形なので,特性方程式を求めると
よって,
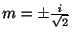 . これより
初期条件
. これより
初期条件
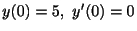 より
より





: 演習問題
: 線形微分方程式
: 演習問題
目次
索引
Administrator
平成26年9月18日
![]() の根は
の根は
![]() .よって
.よって
![]() は解である.またこの2つの関数は例題2.2より一次独立.したがって一般解は
は解である.またこの2つの関数は例題2.2より一次独立.したがって一般解は
![]() の根は
の根は![]() .よって
.よって
![]() は解である.
この微分方程式は2階なので一般解を得るには一次独立な解がもうひとつ必要である.
演習問題2.2.1よりもうひとつの解
は解である.
この微分方程式は2階なので一般解を得るには一次独立な解がもうひとつ必要である.
演習問題2.2.1よりもうひとつの解![]() を求めると
を求めると
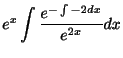
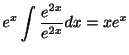
![]() とおく.すると
とおく.すると
![]() は
は![]() の一次独立な解である.よって一般解は
の一次独立な解である.よって一般解は
![]() の係数を実数とします.
の係数を実数とします.![]() が対応する特性方程式
が対応する特性方程式![]() の特性根ならばその共役
の特性根ならばその共役![]() も特性根です.したがって
も特性根です.したがって
![]() の根は
の根は
![]() .よって
.よって
![]() ,バネの弾力定数を
,バネの弾力定数を![]() ,ダッシュポットの摩擦による減衰力は物体の速度
,ダッシュポットの摩擦による減衰力は物体の速度![]() に比例するとき,この物体に働いている力は
に比例するとき,この物体に働いている力は
![]() と加速度
と加速度
![]() の積で表わされます.よって運動方程式
の積で表わされます.よって運動方程式
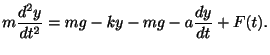
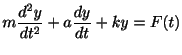
![]() ,バネ定数
,バネ定数
![]() より
より