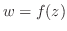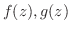Next: 初等関数(elementary functions) Up: 複素関数 Previous: 複素数の関数(complex function) 索引
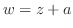 を複素数の定数とするとき,
を複素数の定数とするとき,
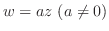
 の 1次分数関数(linear fractional transformation)という.
の 1次分数関数(linear fractional transformation)という.
この関数は,分解すると次の3つの関数の合成であることが分かる.
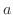 複素平面上で平行移動
複素平面上で平行移動
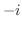 複素平面上で 回転と伸縮
複素平面上で 回転と伸縮
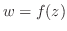 原点を通る直線は原点を通る直線に,その他の直線は原点を通る円に,原点を通る円は直線に,その他の円は円に変換される.
原点を通る直線は原点を通る直線に,その他の直線は原点を通る円に,原点を通る円は直線に,その他の円は円に変換される.
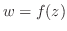 による次の直線または円の像はどんな直線または円に写されるか.
による次の直線または円の像はどんな直線または円に写されるか.
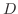 と2点P,Qで交わる直線
と2点P,Qで交わる直線
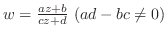 (実数),
(実数),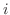 ,
,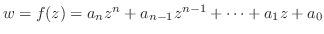 を通る円
を通る円
2. 複素平面上で,次の1次変換による不変な点を求めよ.