Next: 2.4 初等関数の逆関数 Up: 演習問題詳解 Previous: 1次関数 索引
1.
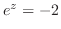 より
より
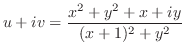 .ここで,複素数が等しいのは実部と虚部どうしが等しいことであることに注意すると,次の連立方程式を得る.
.ここで,複素数が等しいのは実部と虚部どうしが等しいことであることに注意すると,次の連立方程式を得る.
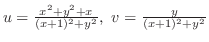
ここで,
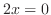 であることに注意すると
であることに注意すると
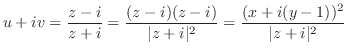
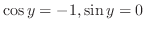 .つまり
.つまり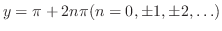 となる.これを上の連立方程式に代入すると
となる.これを上の連立方程式に代入すると
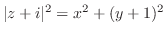 となり,これより
となり,これより
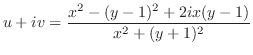 を得る.よって求める
を得る.よって求める は
は
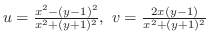
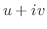 より
より
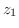 .ここで,複素数が等しいのは実部と虚部どうしが等しいことであることに注意すると,次の連立方程式を得る.
.ここで,複素数が等しいのは実部と虚部どうしが等しいことであることに注意すると,次の連立方程式を得る.
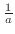
ここで,
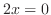 であることに注意すると
であることに注意すると
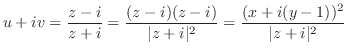
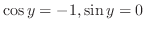 .つまり
.つまり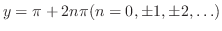 となる.これを上の連立方程式に代入すると
となる.これを上の連立方程式に代入すると
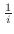 となり,これより
となり,これより
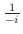 を得る.よって求める
を得る.よって求める は
は
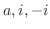
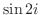 より
より
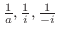 .ここで,複素数が等しいのは実部と虚部どうしが等しいことであることに注意すると,次の連立方程式を得る.
.ここで,複素数が等しいのは実部と虚部どうしが等しいことであることに注意すると,次の連立方程式を得る.
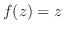
ここで,
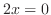 であることに注意すると
であることに注意すると
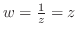
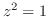 .つまり
.つまり
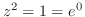 となる.これを上の連立方程式に代入すると
となる.これを上の連立方程式に代入すると
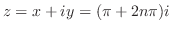 となり,これより
となり,これより
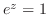 を得る.よって求める
を得る.よって求める は
は
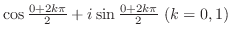
(a) 三角関数はいったん指数関数を用いて書き直す.その後極形式を直交形式に直せばよい.
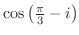 を指数関数を用いて表すと
を指数関数を用いて表すと
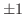
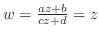
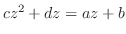 |
 |
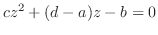 |
|
 |
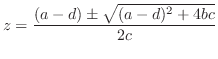 |
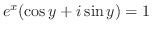 |
 |
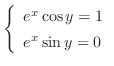 |
|
 |
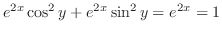 |
||
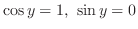 |
|||
 |
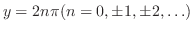 |
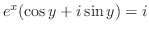 |
 |
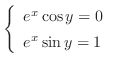 |
|
 |
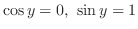 |
||
 |
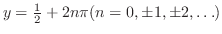 |
||
 |
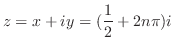 |
||
 |
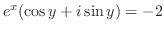 |
||
 |
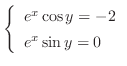 |
||
 |
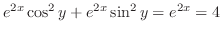 |
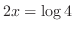
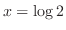
3.
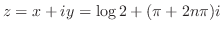 の両辺を
の両辺を
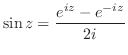 で割ると
で割ると
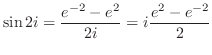
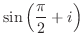
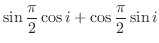
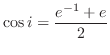
4.
(a)
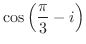 を満たす
を満たす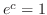 のうち
のうち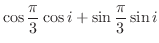 が最小のものを関数
が最小のものを関数 の周期という.また,
の周期という.また,
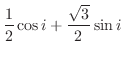 であることに注意する.
であることに注意する.
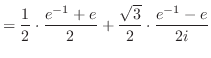 とおいて
とおいて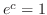 の値を求める.
の値を求める.
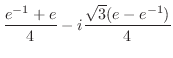 より,
より,
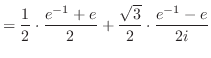 おくと
おくと
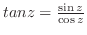 |
 |
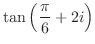 |
|
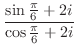 |
 |
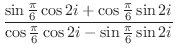 |
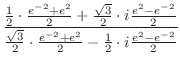 が共通項であることが分かる.したがって,
が共通項であることが分かる.したがって,
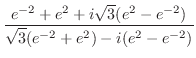
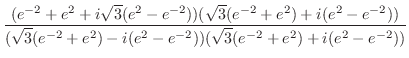
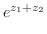 であることを用いると,
であることを用いると,
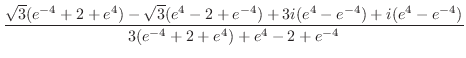 より
より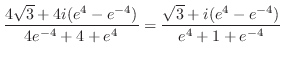 .また,
.また,
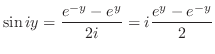 より
より
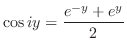
5.
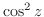 |
 |
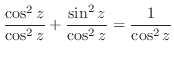 |
|
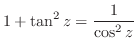 |
 |
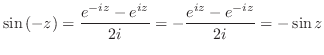 |
|
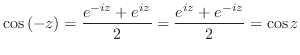 |
 |
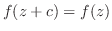 |
|
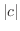 |
 |
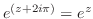 |
|
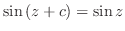 |
 |
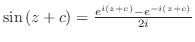 |
|
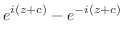 |
 |
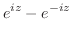 |
|
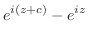 |
 |
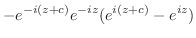 |
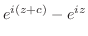 .したがって,
.したがって,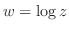 は周期
は周期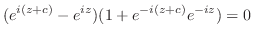 を持つ.
を持つ.