Next: 極限と連続 Up: 演習問題詳解 Previous: 2.3 初等関数 索引
1.
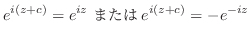 とは
とは
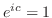 を表す.したがって2価関数である.ここで,
を表す.したがって2価関数である.ここで,
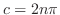 とすると
とすると
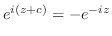
2.
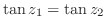
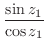
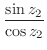
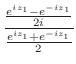
3.
![$\displaystyle (-1)^{i} = e^{i\log{(-1)}} = e^{i [\log_{e}{\vert-1\vert} + i(\pi + 2n\pi)]} = e^{-(2n+1)\pi}$](img697.png)
![$\displaystyle (i)^{i} = e^{i\log{(i)}} = e^{i [\log_{e}{\vert i\vert} + i(\frac{\pi}{2} + 2n\pi)]} = e^{-(2n+\frac{1}{2})\pi}$](img698.png)
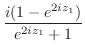 |
 |
![$\displaystyle e^{i\log{(2)}} = e^{i [\log_{e}{\vert 2\vert} + i(0 + 2n\pi)]}$](img700.png) |
|
 |
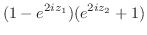 |
||
 |
![$\displaystyle e^{-2n\pi}[\cos{(\log_{e}{2})}+i \sin{(\log_{e}{2})}]$](img702.png) |
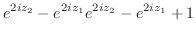 |
 |
![$\displaystyle 2\cdot2^{i} = 2e^{i\log{(2)}} = 2e^{i [\log_{e}{\vert 2\vert} + i(0 + 2n\pi)]}$](img704.png) |
|
 |
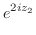 |
||
 |
![$\displaystyle 2e^{-2n\pi}[\cos{(\log_{e}{2})}+i \sin{(\log_{e}{2})}]$](img706.png) |
4.
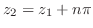 とおくと
とおくと
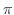 .ここで複素関数
.ここで複素関数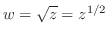 は指数関数を用いて定義されていることに注意すると,
は指数関数を用いて定義されていることに注意すると,
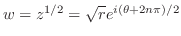
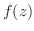 について解けばよい.
について解けばよい.
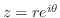 |
 |
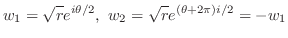 |
|
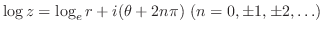 |
 |
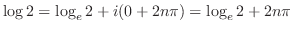 |
|
| 0 |  |
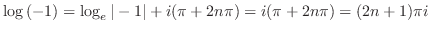 |
|
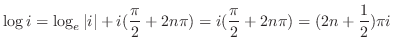 |
 |
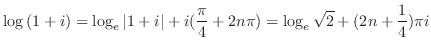 |
|
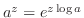 |
 |
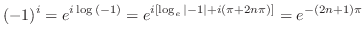 |
|
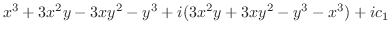 |
 |
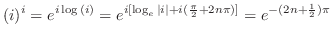 |
注意
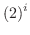 は2価性によって根号の前に
は2価性によって根号の前に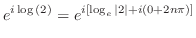 のついた2つの分枝を同時に表しているものとすれば,
のついた2つの分枝を同時に表しているものとすれば,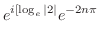 だけでよい.
だけでよい.
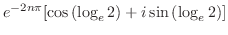 とおくと
とおくと
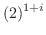 .ここで複素関数
.ここで複素関数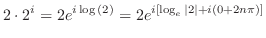 は指数関数を用いて定義されていることに注意すると,
は指数関数を用いて定義されていることに注意すると,
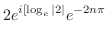
 について解けばよい.
について解けばよい.
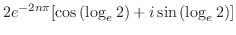 |
 |
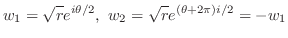 |
|
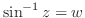 |
 |
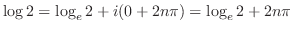 |
|
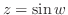 |
 |
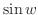 |
|
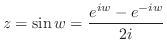 |
 |
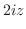 |
|
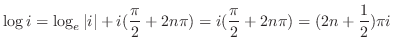 |
 |
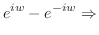 |
|
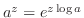 |
 |
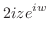 |
|
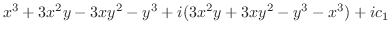 |
 |
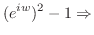 |
5.
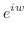
別解
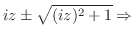 とおくと
とおくと
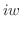 これを
これを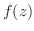 について解くと
について解くと
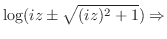 |
 |
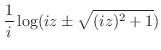 |
|
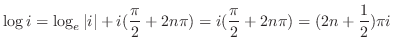 |
 |
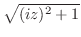 |
|
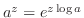 |
 |
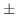 |
|
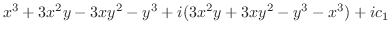 |
 |
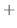 |
注意
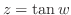
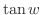
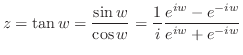 |
 |
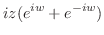 |
|
 |
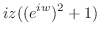 |
||
 |
![$\displaystyle \frac{1}{i}(\log{(i)} + \log{(2 \pm \sqrt{3})}) = \frac{1}{i}[i(2n + \frac{1}{2})\pi + \log_{e}{(2 \pm \sqrt{3})} + i(2n\pi)]$](img752.png) |
||
 |
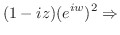 |
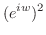 |
 |
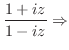 |
|
 |
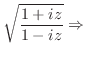 |
ここで
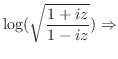
![$\displaystyle \cos^{-1}{(i)} = \left\{\begin{array}{l}
-i[(2n + \frac{1}{2})\pi...
...}) ] \\
-i[(2n + \frac{3}{2})\pi + \log_{e}(\sqrt{2} - 1) ]
\end{array}\right.$](img758.png)