Next: 3.2 正則関数 Up: 演習問題詳解 Previous: 2.4 初等関数の逆関数 索引
1.
集合 が領域とよばれるには次の2つを満たす必要がある.
が領域とよばれるには次の2つを満たす必要がある.
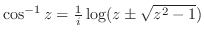
注意
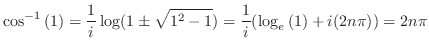 を点
を点 の
の 近傍という.
近傍という.
1. 原点以外の点 を選び,
を選び,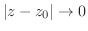 と原点までの距離の半分
と原点までの距離の半分 を
を とすれば,
とすれば, 近傍
近傍
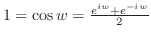 は
は に含まれる.したがって
に含まれる.したがって は開集合.
は開集合.
2. 内のいかなる2点を選んでも
内のいかなる2点を選んでも に含まれる連続な曲線で結ぶことができるので,弧状連結性が満たされる.
に含まれる連続な曲線で結ぶことができるので,弧状連結性が満たされる.
したがって, は領域
は領域
1. 原点以外の点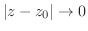 を選び,
を選び,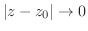 と虚軸までの距離の半分を
と虚軸までの距離の半分を とすれば,
とすれば, 近傍
近傍
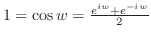 は
は に含まれる.したがって
に含まれる.したがって は開集合.
は開集合.
2. 内のいかなる2点を選んでも
内のいかなる2点を選んでも に含まれる連続な曲線で結ぶことができるので,弧状連結性が満たされる.
に含まれる連続な曲線で結ぶことができるので,弧状連結性が満たされる.
したがって, は領域
は領域
1. 実軸上に点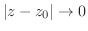 を選ぶと,どんな
を選ぶと,どんな 近傍
近傍
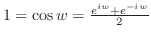 も
も 以外の点を含むので開集合ではない.しかし,
以外の点を含むので開集合ではない.しかし,
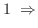 内のどの点を選んでも,その点の
内のどの点を選んでも,その点の 近傍は
近傍は に属する点と属さない点の両方を含む.このような点の集まりを
に属する点と属さない点の両方を含む.このような点の集まりを の 境界という. したがって,
の 境界という. したがって, は閉集合である.
は閉集合である.
2. 内のいかなる2点を選んでも
内のいかなる2点を選んでも に含まれる連続な曲線で結ぶことができるので,弧状連結性が満たされる.
に含まれる連続な曲線で結ぶことができるので,弧状連結性が満たされる.
したがって, は閉領域である.
は閉領域である.
1. 原点以外の点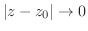 を選び,
を選び,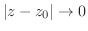 と
と または
または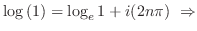 までの距離短い方の半分を
までの距離短い方の半分を とすれば,
とすれば, 近傍
近傍
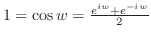 は
は に含まれる.したがって
に含まれる.したがって は開集合.
は開集合.
2. 内のいかなる2点を選んでも
内のいかなる2点を選んでも に含まれる連続な曲線で結ぶことができるので,弧状連結性が満たされる.
に含まれる連続な曲線で結ぶことができるので,弧状連結性が満たされる.
したがって, は領域
は領域
2.
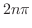
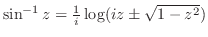
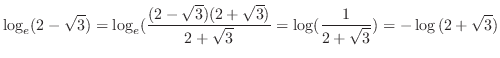
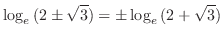
3.
注意
1. 複素平面上の全ての点で指数関数 は連続,原点以外で対数関数
は連続,原点以外で対数関数 は連続,分母が0以外で有理関数は連続
は連続,分母が0以外で有理関数は連続
2. 連続関数の和,差,積,合成はまた連続,分母が0以外で商も連続.
(e)
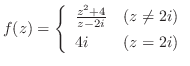 は有理関数.したがって分母が0となる点で不連続.つまり
は有理関数.したがって分母が0となる点で不連続.つまり
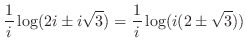 の解となる点で不連続.
の解となる点で不連続.
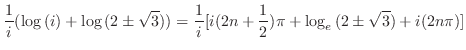
したがって,
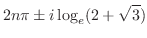
(g)
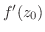 は
は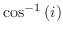 以外では有理関数.したがって分母が0となる点
以外では有理関数.したがって分母が0となる点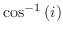 以外では連続.では分母が0となる点で連続だろうか.
以外では連続.では分母が0となる点で連続だろうか.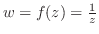 は区分的関数.したがって連続性を調べるには定義に戻る必要がある.つまり
は区分的関数.したがって連続性を調べるには定義に戻る必要がある.つまり
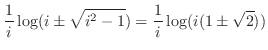
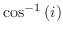 で連続である.
で連続である.
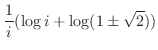
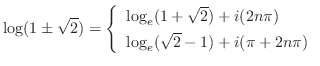 より点
より点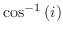 でも連続である.
でも連続である.