Next: 複素関数 Up: 複素数 Previous: 複素数と複素平面(Complex numbers and Complex 索引
ドゥモワブルの定理
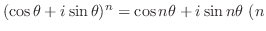 は定数
は定数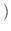
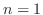 のとき,この式が成り立つのは明らか.
のとき,この式が成り立つのは明らか.
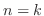 で成り立つと仮定し,
で成り立つと仮定し,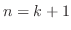 で成り立つことを示す.
で成り立つことを示す.
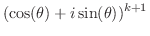 |
 |
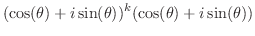 |
|
 |
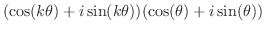 |
||
 |
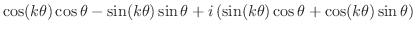 |
||
 |
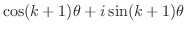 |
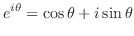
証明
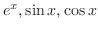 のマクローリン展開は
のマクローリン展開は
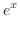 |
 |
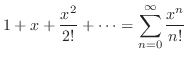 |
|
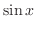 |
 |
 |
|
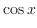 |
 |
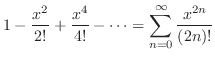 |
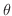 に対して
に対して
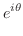 |
 |
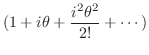 |
|
 |
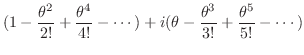 |
||
 |
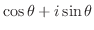 |
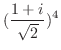
解 極形式に直す.
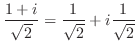
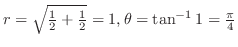 . したがって,
. したがって,
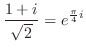
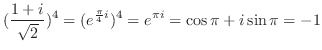
(1)
(2)
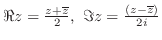
(3)
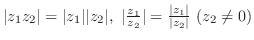
(4)
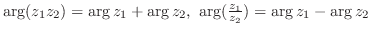
(5)
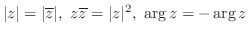
(6)
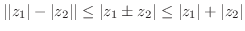
(7) 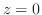 と
と 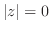 とは同値 (
とは同値 (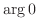 は不定)
は不定)
(8)
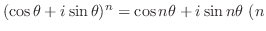 は定数
は定数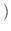 ドゥモワブルの定理
ドゥモワブルの定理
(9)
2項方程式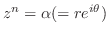 の解は次の
の解は次の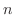 個である.
個である.
![$\displaystyle z_{k} = \sqrt[n]{r}\left(\cos{\frac{\theta + 2k\pi}{n}} + i\sin{\frac{\theta + 2k\pi}{n}}\right) \ (k = 0,1,2.\ldots,n-1)$](img98.png)
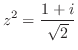
解 2項方程式の解の公式を利用する.
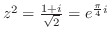 より,その解は
より,その解は
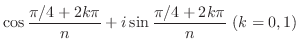
2. 次の複素数を簡単にせよ.
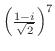
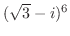
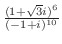
3. 次の方程式を解け.
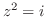
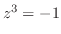
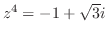
4. 次の値を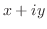 の形(直交形式)で表わせ.
の形(直交形式)で表わせ.
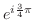
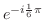
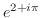
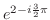
5. 次の複素数を
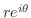 の形(極形式)で表わせ.
の形(極形式)で表わせ.
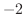
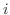
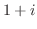
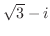
(6) 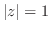 であるための必要十分条件は
であるための必要十分条件は
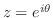 の形に表わせることである.これを証明せよ.
の形に表わせることである.これを証明せよ.