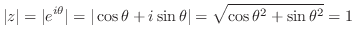Next: 2.1 複素数の関数 Up: 演習問題詳解 Previous: 1.1 複素数と複素平面 索引
1.
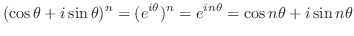
2.
(a) 累乗を含んでいる場合,括弧の中を一度極形式に直すとよい.
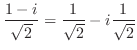
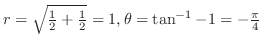 .したがって
.したがって
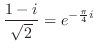
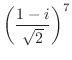 |
 |
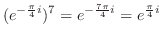 |
|
 |
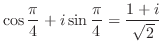 |
(b) 累乗を含んでいる場合,括弧の中を一度極形式に直すとよい.
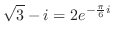
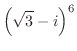 |
 |
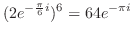 |
|
 |
![$\displaystyle 64[\cos{\pi} - i \sin{\pi}] = -64$](img561.png) |
(c) 累乗を含んでいる場合,括弧の中を一度極形式に直すとよい.
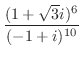 |
 |
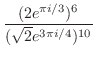 |
|
 |
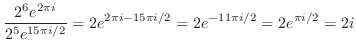 |
3.
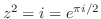 から根は
から根は
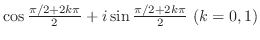
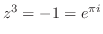 から根は
から根は
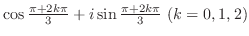
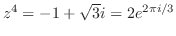 から根は
から根は
![$2^{1/4}[\cos{\frac{2\pi/3 + 2k\pi}{4}} + i\sin{\frac{2\pi/3 + 2k\pi}{4}}] \ (k = 0,1,2,3)$](img570.png)
4.
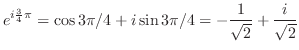
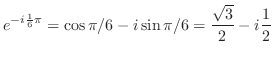
![$\displaystyle e^{2 + i\pi} = e^2 e^{i \pi} = e^{2}[\cos{\pi} + i \sin{\pi} ]= -e^{2}$](img573.png)
![$\displaystyle e^{2 - i\frac{3}{2}\pi} = e^2 e^{-i\frac{3}{2}\pi} = e^{2}[\cos{3\pi/2} - i \sin{3\pi/2}]= e^{2}i$](img574.png)
5.
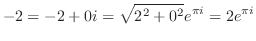
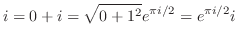
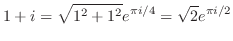
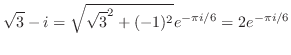
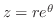 とおくと,
とおくと,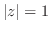 より
より
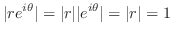
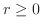 より
より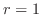 となり
となり
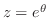 であることが示せた.
であることが示せた.
次に,
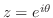 ならば,
ならば,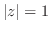 を示す.
を示す.