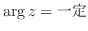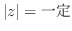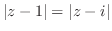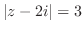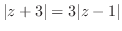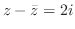Next: ドゥモワブルの定理とオイラーの公式(De Moivre's theorem and Up: 複素数 Previous: 複素数 索引
複素数
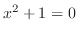 の解は実数
の解は実数 上では存在しない.そこで,この方程式が解けるようにするために虚数単位
上では存在しない.そこで,この方程式が解けるようにするために虚数単位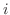 が導入された.つまり,
が導入された.つまり,
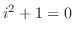 となったわけである.
となったわけである.
虚数単位を取り入れることにより,複素数(complex number)とよばれる新しい数の体系ができた.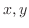 を実数とする.これを
を実数とする.これを
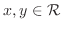 と表わし,
と表わし,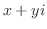 を複素数という.
を複素数という.
複素数の演算は,実数の演算と同じで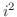 を
を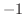 で置き換えればよい.
で置き換えればよい.
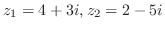 とするとき,以下のものを直交形式で求めよ.
とするとき,以下のものを直交形式で求めよ.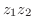 (b)
(b) 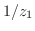 (c)
(c)
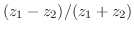
解 (a)
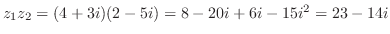
(b)
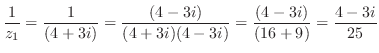
(c)
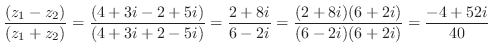
複素平面
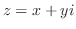 を平面上の直交座標形の点
を平面上の直交座標形の点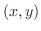 に対応させたとき,この平面を複素平面(complex plane)または,Gauss平面という.
に対応させたとき,この平面を複素平面(complex plane)または,Gauss平面という.
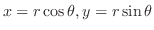 で定義される極座標
で定義される極座標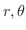 を利用すると,
を利用すると,
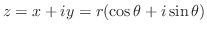 で表され,これを極形式(polar form) という.
で表され,これを極形式(polar form) という.
 の絶対値は
の絶対値は
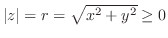 .また,原点と
.また,原点と を結ぶ半直線が実軸となす角
を結ぶ半直線が実軸となす角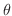 を偏角(argument)といい,偏角 は
を偏角(argument)といい,偏角 は
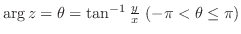 で表わされる.
で表わされる.
(a) 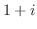 , (b)
, (b)
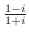
解 (a) 直交形式から極形式への変換は,
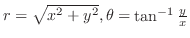 . ただし,
. ただし,
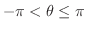 .
.
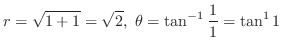 より,
より,
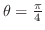 .したがって,
.したがって,
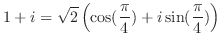
(b)
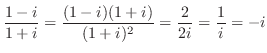 . これより,
. これより,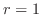 ,
,
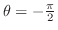 . これより,
. これより,
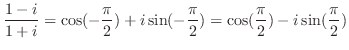
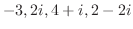 を図示せよ.
を図示せよ.
2. 次の定理を証明せよ.
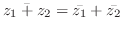
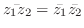
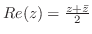
3. 次の不等式を証明せよ.
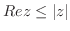
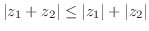
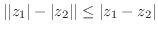
4. 次の複素数を極形式で表わせ.
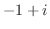
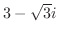
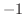
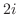
5. 次の式を満たす点はどのような曲線を描くか.