Next: 4.1 級数の定義 Up: 確認問題詳解 Previous: 3.9 定積分の定義の拡張 索引
1.
(a)
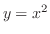 と
と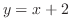 の交点を求めると
の交点を求めると
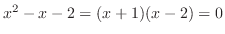 より
より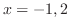 となる.つまり,この2つの曲線は点
となる.つまり,この2つの曲線は点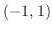 と点
と点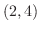 で交わっている.そこでこの図形の面積は縦方向の長方形の面積
で交わっている.そこでこの図形の面積は縦方向の長方形の面積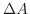 の和として考える.
の和として考える. 軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また幅は
軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また幅は 軸方向への小さな幅となるので
軸方向への小さな幅となるので 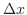 で与えられる.よって
で与えられる.よって
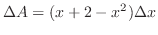
 は
は
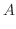 |
 |
![$\displaystyle \int_{-1}^{2}(x+2-x^2)dx = [\frac{x^2}{2} + 2x - \frac{x^3}{3}]_{-1}^{2}$](img1992.png) |
|
 |
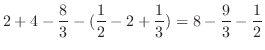 |
||
 |
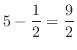 |
(b)
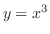 と
と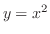 の交点を求めると
の交点を求めると
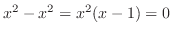 より
より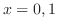 となる.つまり,この2つの曲線は点
となる.つまり,この2つの曲線は点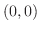 と点
と点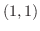 で交わっている.そこでこの図形の面積は縦方向の長方形の面積
で交わっている.そこでこの図形の面積は縦方向の長方形の面積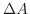 の和として考える.
の和として考える. 軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また幅は
軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また幅は 軸方向への小さな幅となるので
軸方向への小さな幅となるので 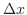 で与えられる.よって
で与えられる.よって
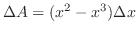
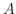 は
は
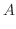 |
 |
![$\displaystyle \int_{0}^{1}(x^2 - x^3)dx = [\frac{x^3}{3} - \frac{x^4}{4}]_{0}^{1}$](img1999.png) |
|
 |
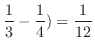 |
(c)
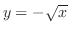 と
と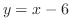 の交点を求めると
の交点を求めると
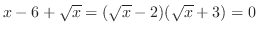 より
より
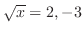 となる.しかし,
となる.しかし,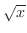 は負の値を取らないので,
は負の値を取らないので,
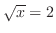 .したがって,
.したがって,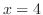 .つまり,この2つの曲線は点
.つまり,この2つの曲線は点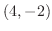 で交わっている.次に,
で交わっている.次に,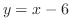 と
と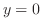 の交点を求めると,
の交点を求めると,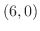 .最後に,
.最後に,
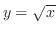 と
と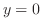 の交点を求めると
の交点を求めると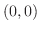 となる.そこでこの図形の面積を縦方向の長方形の面積
となる.そこでこの図形の面積を縦方向の長方形の面積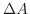 の和として考える.
の和として考える. 軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また幅は
軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また幅は 軸方向への小さな幅となるので
軸方向への小さな幅となるので 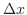 で与えられる.よって区間
で与えられる.よって区間![$[0,4]$](img2009.png) では
では
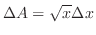
![$[4,6]$](img2011.png) では
では
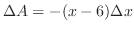
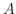 は
は
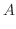 |
 |
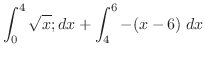 |
|
 |
![$\displaystyle [\frac{2}{3}x^[\frac{3}{2}]_{0}^{4} - [\frac{x^2}{2} - 6x]_{4}^{6}$](img2014.png) |
||
 |
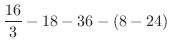 |
||
 |
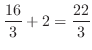 |
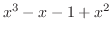 |
 |
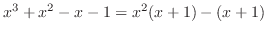 |
|
 |
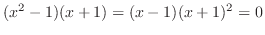 |
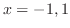 となる.つまり,この2つの曲線は点
となる.つまり,この2つの曲線は点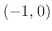 と点
と点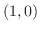 で交わっている.そこでこの図形の面積を縦方向の長方形の面積
で交わっている.そこでこの図形の面積を縦方向の長方形の面積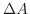 の和として考える.
の和として考える. 軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また幅は
軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また幅は 軸方向への小さな幅となるので
軸方向への小さな幅となるので 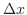 で与えられる.よって
で与えられる.よって
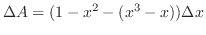
 は
は
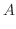 |
 |
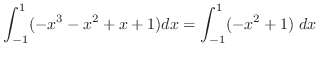 |
|
 |
![$\displaystyle 2\int_{0}^{1}(-x^2 + 1)\;dx = 2[-\frac{x^3}{3} + x]_{0}^{1}$](img2025.png) |
||
 |
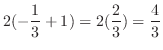 |
(e)
 と
と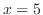 の交点を求めると
の交点を求めると
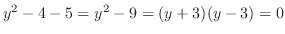 より,
より,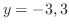 となる.つまり,この2つの曲線は点
となる.つまり,この2つの曲線は点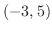 と点
と点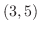 で交わっている.そこでこの図形の面積を横方向の長方形の面積
で交わっている.そこでこの図形の面積を横方向の長方形の面積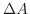 の和として考える.
の和として考える.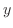 軸に垂直な直線でこの図形を切断するとその幅は,左側の曲線 - 右側の曲線で与えられ,また高さは
軸に垂直な直線でこの図形を切断するとその幅は,左側の曲線 - 右側の曲線で与えられ,また高さは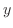 軸方向への小さな幅となるので
軸方向への小さな幅となるので 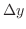 で与えられる.よって
で与えられる.よって
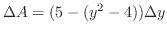
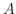 は
は
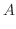 |
 |
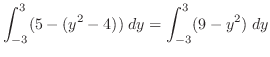 |
|
 |
![$\displaystyle 2\int_{0}^{3}(9 - y^2)\;dy = 2[9y -\frac{y^3}{3} + x]_{0}^{3}$](img2036.png) |
||
 |
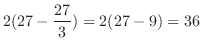 |
(f)
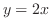 と
と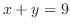 の交点を求めると
の交点を求めると
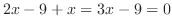 より,
より,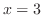 となる.つまり,この2つの曲線は点
となる.つまり,この2つの曲線は点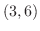 で交わっている.次に,
で交わっている.次に,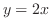 とy
とy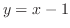 の交点を求めると
の交点を求めると
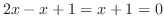 より,点
より,点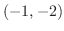 で交わる.最後に,
で交わる.最後に,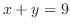 と
と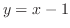 の交点を求めると
の交点を求めると
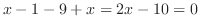 より点
より点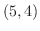 で交わる.そこでこの図形の面積を縦方向の長方形の面積
で交わる.そこでこの図形の面積を縦方向の長方形の面積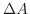 の和として考える.
の和として考える. 軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また高さは
軸に垂直な直線でこの図形を切断するとその高さは,上側の曲線 - 下側の曲線で与えられ,また高さは 軸方向への小さな幅となるので
軸方向への小さな幅となるので 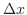 で与えられる.よって区間
で与えられる.よって区間![$[-1,3]$](img2048.png) では,
では,
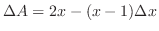
![$[3,5]$](img2050.png) では,
では,
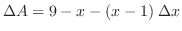
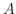 は
は
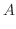 |
 |
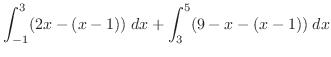 |
|
 |
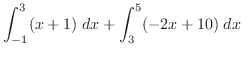 |
||
 |
![$\displaystyle [\frac{x^2}{2} + x]_{-1}^{3} + [-x^2 + 5x]_{3}^{5}$](img2054.png) |
||
 |
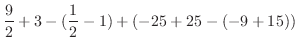 |
||
 |
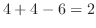 |
2.
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren3-10-2a.eps}
\end{figure}](img2057.png)
 と
と の交点を求めると
の交点を求めると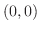 .また,
.また,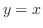 と
と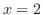 の交点を求めると
の交点を求めると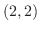 .
回転軸に垂直な平面で切断すると,その断面は円盤になる.円盤の面積は
.
回転軸に垂直な平面で切断すると,その断面は円盤になる.円盤の面積は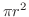 .
よって,
.
よって, 軸上の任意の点
軸上の任意の点 における断面積
における断面積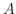 は
は
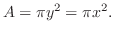
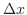 をつけると,その体積
をつけると,その体積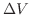 は
は
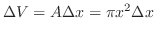
![$\displaystyle V = \int_{0}^{2} \pi x^2\; dx = [\frac{\pi x^3}{3}]_{0}^{1} = \frac{\pi}{3}$](img2063.png)
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren3-10-2b.eps}
\end{figure}](img2064.png)
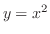 と
と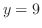 の交点を求めると,
の交点を求めると,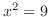 より,
より,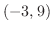 と
と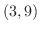 となる.
回転軸に垂直な平面で切断すると,その断面はワッシャーになる.
よって,
となる.
回転軸に垂直な平面で切断すると,その断面はワッシャーになる.
よって, 軸上の任意の点
軸上の任意の点 における断面積
における断面積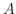 は
は
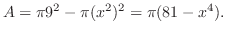
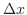 をつけると,その体積
をつけると,その体積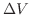 は
は
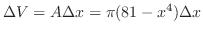
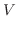 |
 |
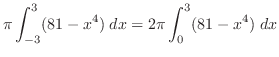 |
|
 |
![$\displaystyle 2\pi [81x - \frac{x^5}{5}]_{0}^{3} = 2\pi(243 - \frac{243}{5})$](img2073.png) |
||
 |
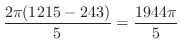 |
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren3-10-2c.eps}
\end{figure}](img2075.png)
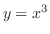 と
と
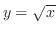 の交点を求めると,
の交点を求めると,
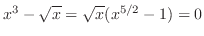 より,
より,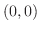 と
と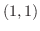 となる.
回転軸に垂直な平面で切断すると,その断面はワッシャーになる.
よって,
となる.
回転軸に垂直な平面で切断すると,その断面はワッシャーになる.
よって, 軸上の任意の点
軸上の任意の点 における断面積
における断面積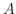 は
は
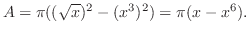
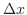 をつけると,その体積
をつけると,その体積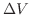 は
は
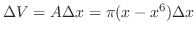
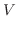 |
 |
![$\displaystyle \pi \int_{0}^{1}(x - x^6)\; dx = \pi [\frac{x^2}{2} - \frac{x^7}{7}]_{0}^{1}$](img2079.png) |
|
 |
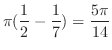 |
![\begin{figure}\includegraphics[width=5cm]{CALCFIG/ren3-10-2d.eps}
\end{figure}](img2081.png)
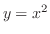 と
と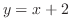 の交点を求めると,
の交点を求めると,
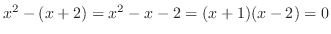 より,
より,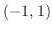 と
と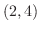 となる.
回転軸に垂直な平面で切断すると,その断面はワッシャーになる.
よって,
となる.
回転軸に垂直な平面で切断すると,その断面はワッシャーになる.
よって, 軸上の任意の点
軸上の任意の点 における断面積
における断面積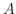 は
は
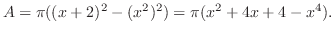
 をつけると,その体積
をつけると,その体積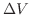 は
は
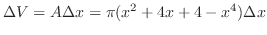
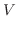 |
 |
![$\displaystyle \pi \int_{-1}^{2}(x^2 + 4x + 4 - x^4)\; dx = \pi [\frac{x^3}{3} + 2x^2 + 4x - \frac{x^5}{5}]_{-1}^{2}$](img2085.png) |
|
 |
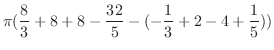 |
||
 |
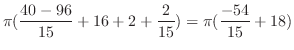 |
||
 |
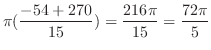 |
3.
曲線の1部分 は
は
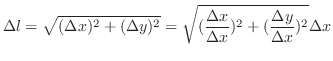
 |
 |
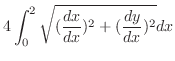 |
|
 |
![$\displaystyle \int_{0}^{2}\sqrt{1 + 2^2} dx = [\sqrt{5}x]_{0}^{2}$](img2093.png) |
||
 |
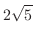 |
曲線の1部分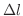 は
は
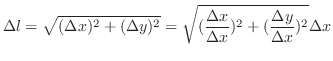
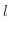 |
 |
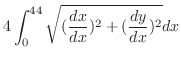 |
|
 |
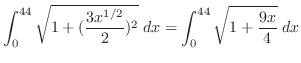 |
||
 |
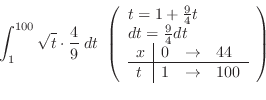 |
||
 |
![$\displaystyle \frac{4}{9}\cdot \frac{2}{3}[t^{3/2}]_{1}^{100} = \frac{8}{27}(1000 - 1)$](img2098.png) |
||
 |
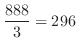 |
曲線の1部分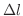 は
は
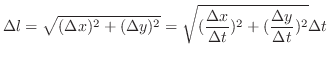
 |
 |
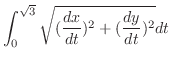 |
|
 |
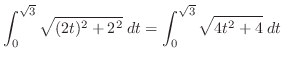 |
||
 |
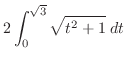 |
||
 |
![$\displaystyle 2[t\sqrt{t^2 + 1} + \log\vert t + \sqrt{t^2 + 1}\vert]_{0}^{\sqrt{3}}$](img2104.png) |
||
 |
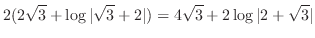 |
曲線の1部分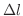 は
は
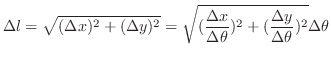
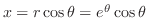 ,
,
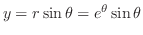 より
より
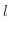 |
 |
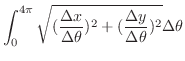 |
|
 |
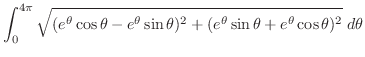 |
||
 |
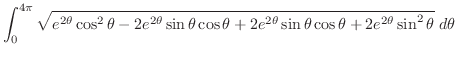 |
||
 |
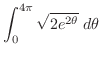 |
||
 |
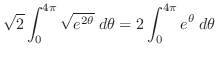 |
||
 |
![$\displaystyle \sqrt{2}[e^{\theta}]_{0}^{4\pi} = \sqrt{2}(e^{4\pi} - 1)$](img2114.png) |