3.9 定積分の定義の拡張

積分範囲が有限でないので，まず，積分範囲を1から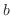 $b$

までとし，積分を行ったあと $b$

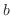を無限大に持って行く．

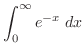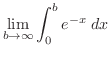$\displaystyle \int_{0}^{\infty}e^{-x}\; dx$	$\displaystyle =$	$\displaystyle \lim_{b \to \infty}\int_{0}^{b}e^{-x}\;dx$
	$\displaystyle =$	$\displaystyle \lim_{b \to \infty}\left[-e^{-x}\right]_{0}^{b} = \lim_{b \to \infty}(-e^{-b} + 1)$
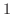	$\displaystyle =$	$\displaystyle 1$

積分範囲が有限でないので，まず，積分範囲を1から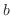 $b$

までとし，積分を行ったあと $b$

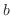を無限大に持って行く．

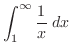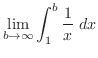$\displaystyle \int_{1}^{\infty}\frac{1}{x}\; dx$	$\displaystyle =$	$\displaystyle \lim_{b \to \infty}\int_{1}^{b}\frac{1}{x}\;dx$
	$\displaystyle =$	$\displaystyle \lim_{b \to \infty}\left[\log{x}\right]_{1}^{b} = \lim_{b \to \infty}\log{b}$
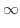	$\displaystyle =$	$\displaystyle \infty$

積分範囲が有限でないので，まず，積分範囲を1から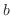 $b$

までとし，積分を行ったあと $b$

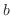を無限大に持って行く．

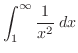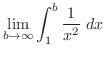$\displaystyle \int_{1}^{\infty}\frac{1}{x^2}\; dx$	$\displaystyle =$	$\displaystyle \lim_{b \to \infty}\int_{1}^{b}\frac{1}{x^2}\;dx$
	$\displaystyle =$	$\displaystyle \lim_{b \to \infty}\left[-\frac{1}{x}\right]_{1}^{b} = \lim_{b \to \infty}(-\frac{1}{b} + 1)$
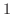	$\displaystyle =$	$\displaystyle 1$

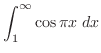$\displaystyle \int_{1}^{\infty}\cos{\pi x}\; dx$	$\displaystyle =$	$\displaystyle \lim_{b \to \infty}[\frac{1}{\pi}\sin{\pi x}]_{1}^{b}$
	$\displaystyle =$	存在しない

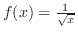$f(x) = \frac{1}{\sqrt{x}}$ は $x = 0$

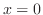で分母が0になる．したがって， $x = 0$

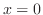で連続ではない．そのため， $x = 0$

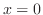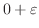の直後 $0 + \varepsilon$ から積分し，その後 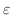$\varepsilon$ を0に近づける．

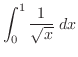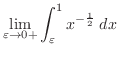$\displaystyle \int_{0}^{1}\frac{1}{\sqrt{x}}\; dx$	$\displaystyle =$	$\displaystyle \lim_{\varepsilon \to 0+}\int_{\varepsilon}^{1}x^{-\frac{1}{2}}\;dx$
	$\displaystyle =$	$\displaystyle \lim_{\varepsilon \to 0+}\left[2x^{\frac{1}{2}}\right]_{\varepsilon}^{1} = \lim_{\varepsilon \to 0+}(2-2\varepsilon^{\frac{1}{2}})$
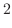	$\displaystyle =$	$\displaystyle 2$

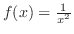$f(x) = \frac{1}{x^2}$ は $x = 0$

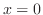で分母が0になる．したがって， $x = 0$

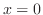で連続ではない．そのため， $x = 0$

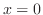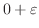の直後 $0 + \varepsilon$ から積分し，その後 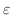$\varepsilon$ を0に近づける．

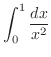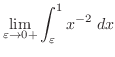$\displaystyle \int_{0}^{1}\frac{dx}{x^2}$	$\displaystyle =$	$\displaystyle \lim_{\varepsilon \to 0+}\int_{\varepsilon}^{1}x^{-2}\;dx$
	$\displaystyle =$	$\displaystyle \lim_{\varepsilon \to 0+}\left[-\frac{1}{x}\right]_{\varepsilon}^{1} = -\lim_{\varepsilon \to 0+}(1 - \frac{1}{\varepsilon})$
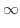	$\displaystyle =$	$\displaystyle \infty$