Next: 3.7 定積分 Up: 確認問題詳解 Previous: 3.5 三角関数の積分法 索引
如何に有理関数に直すかが問題
1.
(a) 無理関数
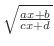 をtとおくことにより,有理関数に直す.
をtとおくことにより,有理関数に直す.
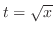 とおくと
とおくと 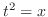 より
より
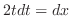 .
したがって,
.
したがって,
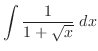 |
 |
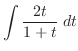 |
|
 |
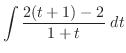 |
||
 |
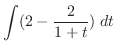 |
||
 |
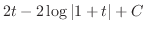 |
||
 |
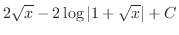 |
(b) 無理関数
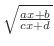 をtとおくことにより,有理関数に直す.
をtとおくことにより,有理関数に直す.
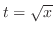 とおくと
とおくと 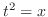 より
より
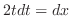 .
したがって,
.
したがって,
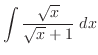 |
 |
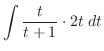 |
|
 |
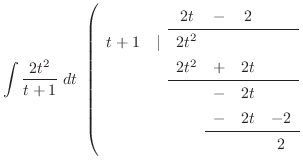 |
||
 |
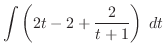 |
||
 |
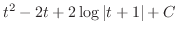 |
||
 |
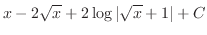 |
(c) 無理関数
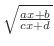 をtとおくことにより,有理関数に直す.
をtとおくことにより,有理関数に直す.
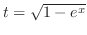 とおくと
とおくと
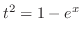 より
より
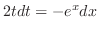 .
したがって,
.
したがって,
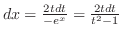 . これより,
. これより,
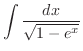 |
 |
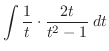 |
|
 |
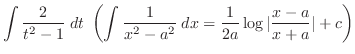 |
||
 |
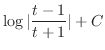 |
||
 |
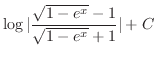 |
(d) 無理関数
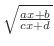 をtとおくことにより,有理関数に直す.
をtとおくことにより,有理関数に直す.
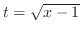 とおくと
とおくと
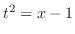 より
より
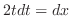 .
したがって,
.
したがって,
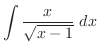 |
 |
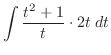 |
|
 |
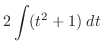 |
||
 |
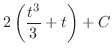 |
||
 |
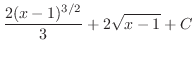 |
(e) 平方根の中が2次関数で分子が奇数次の式なので.
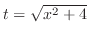 とおくと
とおくと
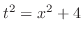 より
より
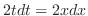 .
したがって,
.
したがって,
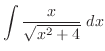 |
 |
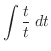 |
|
 |
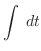 |
||
 |
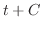 |
||
 |
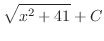 |
別解
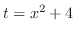 とおくと
とおくと 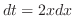 .
したがって,
.
したがって,
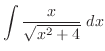 |
 |
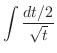 |
|
 |
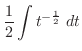 |
||
 |
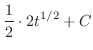 |
||
 |
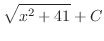 |
(f) 平方根の中が2次関数で分子が奇数次の式なので..
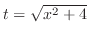 とおくと
とおくと
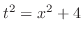 より
より
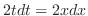 .
したがって,
.
したがって,
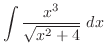 |
 |
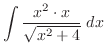 |
|
 |
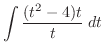 |
||
 |
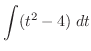 |
||
 |
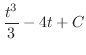 |
||
 |
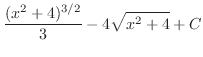 |
(g) 平方根の中が2次関数で分子が偶数次の式なので.次のどちらかに帰着する.
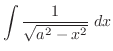 |
 |
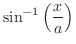 |
|
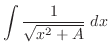 |
 |
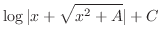 |
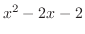 を平方完成すると
を平方完成すると
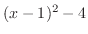 となる.そこで,
となる.そこで,
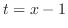 とおくと
とおくと 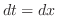 .
したがって,
.
したがって,
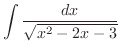 |
 |
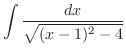 |
|
 |
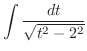 |
||
 |
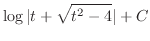 |
||
 |
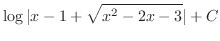 |
(h) 平方根の中が2次関数で分母が奇数次の式なので,
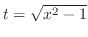 とおくと
とおくと
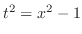 より
より
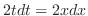 .
したがって,
.
したがって,
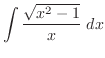 |
 |
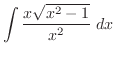 |
|
 |
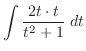 |
||
 |
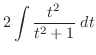 |
||
 |
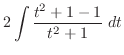 |
||
 |
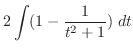 |
||
 |
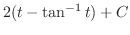 |
||
 |
 |