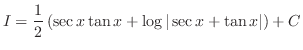3.5 三角関数の積分法

いかに有理関数へ直すかが問題

1.

(a)

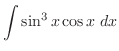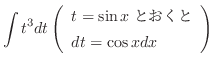$\displaystyle \int{\sin^{3}{x}\cos{x}} \; dx$	$\displaystyle =$	$\displaystyle \int{t^3 dt} \left(\begin{array}{l} t = \sin{x}とおくと\\ dt = \cos{x}dx \end{array}\right)$
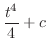	$\displaystyle =$	$\displaystyle \frac{t^4}{4} + c$
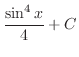	$\displaystyle =$	$\displaystyle \frac{\sin^4{x}}{4} + C$

(b)

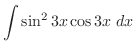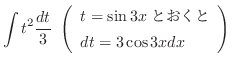$\displaystyle \int{\sin^{2}{3x}\cos{3x}} \; dx$	$\displaystyle =$	$\displaystyle \int{t^2 \frac{dt}{3}} \left(\begin{array}{l} t = \sin{3x}とおくと\\ dt = 3\cos{3x}dx \end{array}\right)$
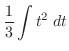	$\displaystyle =$	$\displaystyle \frac{1}{3}\int t^2\; dt$
	$\displaystyle =$	$\displaystyle \frac{t^3}{9} + c$
	$\displaystyle =$	$\displaystyle \frac{\sin^3{3x}}{9} + C$

(c)

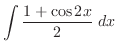$\displaystyle \int{\cos^{2}{x}\cos{3x}} \; dx$	$\displaystyle =$	$\displaystyle \int{\frac{1 + \cos{2x}}{2}\; dx}$
	$\displaystyle =$	$\displaystyle \frac{1}{2}\left[\int (x + \cos{2x})\; dx\right]$
	$\displaystyle =$	$\displaystyle \frac{1}{2}\left[\frac{x^2}{2} + \frac{\sin{2x}}{2}\right] + C$

(d)

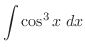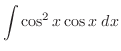$\displaystyle \int{\cos^{3}{x}} \; dx$	$\displaystyle =$	$\displaystyle \int{\cos^2{x}\cos{x}\; dx}$
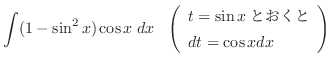	$\displaystyle =$	$\displaystyle \int(1 - \sin^2{x})\cos{x}\; dx \left(\begin{array}{l} t = \sin{x}とおくと\\ dt = \cos{x}dx \end{array}\right)$
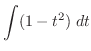	$\displaystyle =$	$\displaystyle \int (1 - t^2)\; dt$
	$\displaystyle =$	$\displaystyle t - \frac{t^3}{3} + C$
	$\displaystyle =$	$\displaystyle \sin{x} - \frac{\sin^3{x}}{3} + C$

(e)

$\displaystyle \int{\cos^{4}{x}\sin^3{x}} \; dx$	$\displaystyle =$	$\displaystyle \int{\cos^4{x}\sin^2{x}\sin{x}\; dx}$
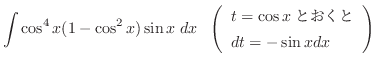	$\displaystyle =$	$\displaystyle \int \cos^4{x}(1 - \cos^2{x})\sin{x}\; dx \left(\begin{array}{l} t = \cos{x}とおくと\\ dt = -\sin{x}dx \end{array}\right)$
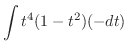	$\displaystyle =$	$\displaystyle \int t^4(1 - t^2)(-dt)$
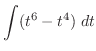	$\displaystyle =$	$\displaystyle \int (t^6 - t^4)\; dt$
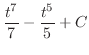	$\displaystyle =$	$\displaystyle \frac{t^7}{7} - \frac{t^5}{5} + C$
	$\displaystyle =$	$\displaystyle \frac{\cos^7{x}}{7} - \frac{\cos^5{x}}{5} + C$

(f)

$\displaystyle \int{\sin{2x}\cos{3x}} \; dx$	$\displaystyle =$	$\displaystyle \frac{1}{2}\int{\sin{5x} - \sin{x}\; dx}$
	$\displaystyle =$	$\displaystyle \frac{1}{2}\left(-\frac{\cos{5x}}{5} + \cos{x}\right) + C$

(g)

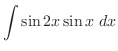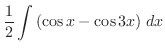$\displaystyle \int{\sin{2x}\sin{x}} \; dx$	$\displaystyle =$	$\displaystyle \frac{1}{2}\int{(\cos{x} - \cos{3x})\; dx}$
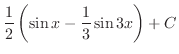	$\displaystyle =$	$\displaystyle \frac{1}{2}\left(\sin{x} - \frac{1}{3}\sin{3x}\right) + C$

(h)

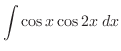$\displaystyle \int{\cos{x}\cos{2x}} \; dx$	$\displaystyle =$	$\displaystyle \frac{1}{2}\int{(\cos{3x} + \cos{x})\; dx}$
	$\displaystyle =$	$\displaystyle \frac{1}{2}\left(\frac{\sin{3x}}{3} + \sin{x}\right) + C$

(i)

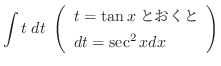$\displaystyle \int{\tan{x}\sec^2{x}} \; dx$	$\displaystyle =$	$\displaystyle \int t\;dt \left(\begin{array}{l} t = \tan{x}とおくと\\ dt = \sec^2{x}dx \end{array}\right)$
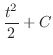	$\displaystyle =$	$\displaystyle \frac{t^2}{2} + C$
	$\displaystyle =$	$\displaystyle \frac{\tan^2{x}}{2} + C$

(j)

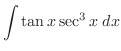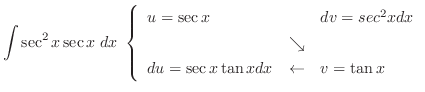$\displaystyle \int{\tan{x}\sec^3{x}} \; dx$	$\displaystyle =$	$\displaystyle \int \sec^2{x}\sec{x}\; dx\ \left\{\begin{array}{lcl} u = \sec{x... ...\searrow& \\ du = \sec{x}\tan{x}dx &\leftarrow& v = \tan{x} \end{array}\right.$
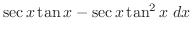	$\displaystyle =$	$\displaystyle \sec{x}\tan{x} - \sec{x}\tan^2{x}\;dx$
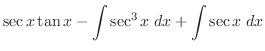	$\displaystyle =$	$\displaystyle \sec{x}\tan{x} - \int \sec^3{x}\; dx + \int \sec{x}\; dx$

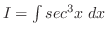ここで， $I = \int sec^3{x}\; dx$ とおくと，

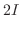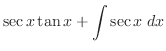$\displaystyle 2I$	$\displaystyle =$	$\displaystyle \sec{x}\tan{x} + \int \sec{x}\;dx$
	$\displaystyle =$	$\displaystyle \sec{x}\tan{x} + \log\vert\sec{x} + \tan{x}\vert + c$

したがって，

$\displaystyle I = \frac{1}{2}\left(\sec{x}\tan{x} + \log\vert\sec{x} + \tan{x}\vert \right) + C$