Next: 3.5 三角関数の積分法 Up: 確認問題詳解 Previous: 3.3 部分積分法 索引
全ての不定積分は有理関数に変形できれば必ず求めることができる.
1.
(a)
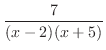 は有理関数で分子の次数
は有理関数で分子の次数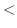 分母の次数なので,部分分数分解すると,
分母の次数なので,部分分数分解すると,
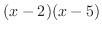 の因数
の因数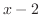 と
と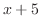 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
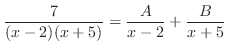
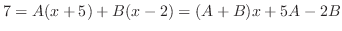
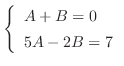
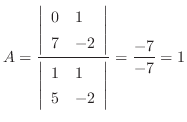
これをもとの式に代入すると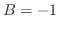 となるので
となるので
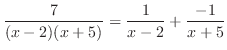
(b)
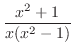 は有理関数で分子の次数
は有理関数で分子の次数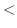 分母の次数なので,部分分数分解すると,
分母の次数なので,部分分数分解すると,
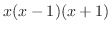 の因数
の因数
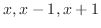 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
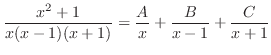
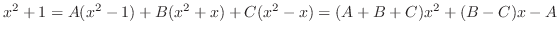
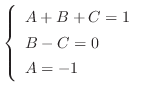
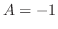 より次の連立方程式を得る.
より次の連立方程式を得る.
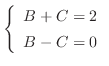
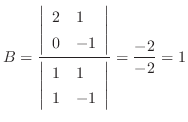
これを上の式に代入すると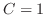 となるので
となるので
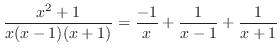
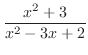 は有理関数で,分子の次数が分母の次数以上なので,まず分子を分母で割ると
は有理関数で,分子の次数が分母の次数以上なので,まず分子を分母で割ると
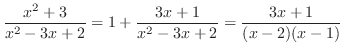
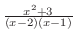 を部分分数分解すると,
を部分分数分解すると,
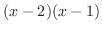 の因数
の因数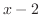 と
と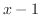 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
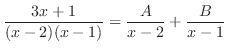
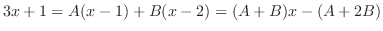
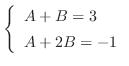
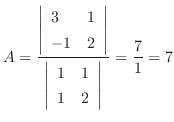
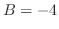 となるので
となるので
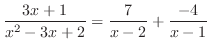
(d)
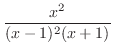 は有理関数で分子の次数
は有理関数で分子の次数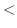 分母の次数なので,部分分数分解すると,
分母の次数なので,部分分数分解すると,
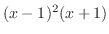 の因数
の因数
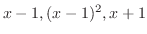 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
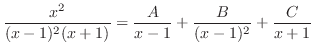
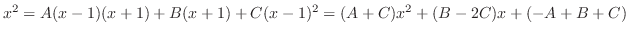
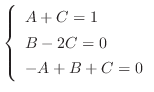
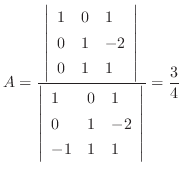
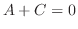 代入すると
代入すると
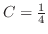 .さらに,
.さらに,
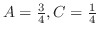 より
より
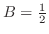 を得る.よって
を得る.よって
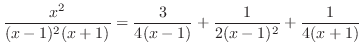
(e)
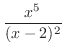 は有理関数で分子の次数
は有理関数で分子の次数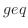 分母の次数なので,まず,分子を分母で割ると,
分母の次数なので,まず,分子を分母で割ると,
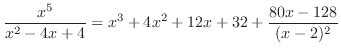
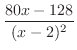 を部分分数分解すると,
を部分分数分解すると,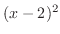 の因数
の因数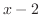 と
と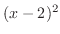 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
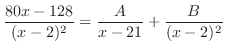
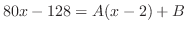
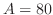 を得る.これを上の式に代入すると,
を得る.これを上の式に代入すると,
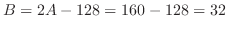 を得る.よって
を得る.よって
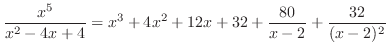
(f)
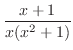 は有理関数で分子の次数
は有理関数で分子の次数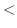 分母の次数なので部分分数分解すると,
分母の次数なので部分分数分解すると,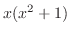 の因数
の因数 と
と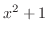 を分母に持つ分数の和で表せる.
を分母に持つ分数の和で表せる.
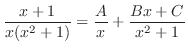
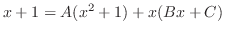
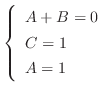
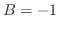 を得る.よって,
を得る.よって,