Next: 1.5 数列 Up: 確認問題詳解 Previous: 1.3 関数の極限 索引
1.
2.
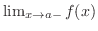 が
が
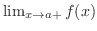 と等しく,さらに
と等しく,さらに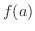 と等しいとき,関数
と等しいとき,関数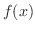 は
は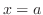 で連続であるという.
で連続であるという.
3.
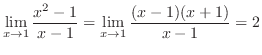 . したがって,
. したがって,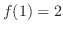 .
.
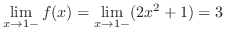 .
.
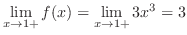 したがって,
したがって,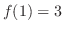 .
.
4.
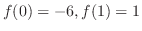 より,
より,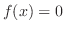 の解は
の解は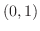 の間にある.そこで,
の間にある.そこで,![$[0,1]$](img146.png) の中点
の中点
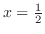 を用いて
を用いて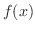 を求めると,
を求めると,
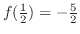 となる.中間値の定理より,解は
となる.中間値の定理より,解は
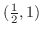 の間にある.そこで,この区間の中点
の間にある.そこで,この区間の中点
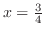 を用いて
を用いて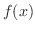 を求めると,
を求めると,
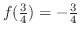 となる.再び中間値の定理より,解は
となる.再び中間値の定理より,解は
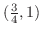 の間にある.そこで,この区間の中点
の間にある.そこで,この区間の中点
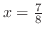 を用いて
を用いて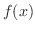 を求めると,
を求めると,
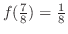 となる.再び中間値の定理より,解は
となる.再び中間値の定理より,解は
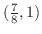 の間にある.そこで,この区間の中点
の間にある.そこで,この区間の中点
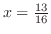 を用いて
を用いて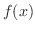 を求めると,
を求めると,
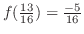 となる.中点を1回取るたびに,近似解と真の解との差は半分ずつになる.したがって,誤差を
となる.中点を1回取るたびに,近似解と真の解との差は半分ずつになる.したがって,誤差を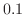 以下にするには,中点を4回とればよい.したがって,近似解は
以下にするには,中点を4回とればよい.したがって,近似解は
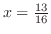 である.
である.