Next: 6.3 解答 Up: 演習問題詳解 Previous: 6.1 解答 索引
6.2
1.
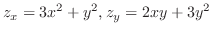
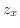 |
 |
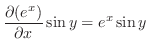 |
|
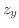 |
 |
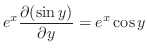 |
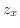 |
 |
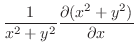 |
|
 |
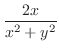 |
||
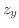 |
 |
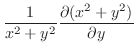 |
|
 |
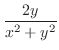 |
2.
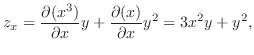
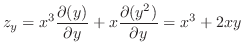
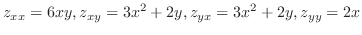
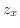 |
 |
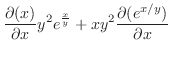 |
|
 |
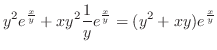 |
||
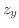 |
 |
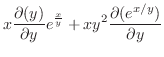 |
|
 |
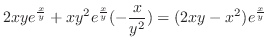 |
||
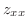 |
 |
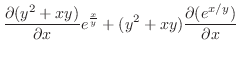 |
|
 |
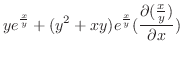 |
||
 |
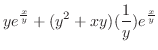 |
||
 |
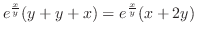 |
||
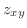 |
 |
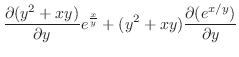 |
|
 |
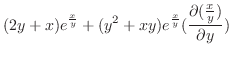 |
||
 |
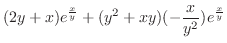 |
||
 |
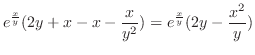 |
||
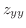 |
 |
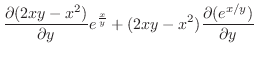 |
|
 |
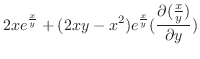 |
||
 |
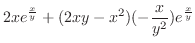 |
||
 |
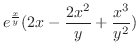 |
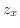 |
 |
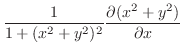 |
|
 |
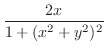 |
||
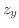 |
 |
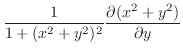 |
|
 |
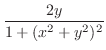 |
||
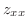 |
 |
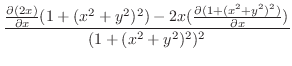 |
|
 |
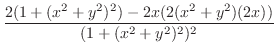 |
||
 |
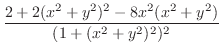 |
||
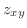 |
 |
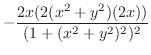 |
|
 |
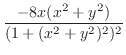 |
||
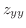 |
 |
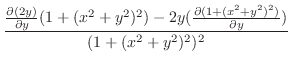 |
|
 |
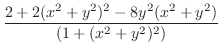 |
3.
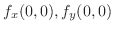 が存在するか調べればよい.
が存在するか調べればよい.
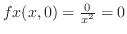 より
より
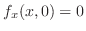 .したがって,
.したがって,
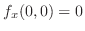 .
.
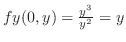 .
.
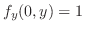 .したがって,
.したがって,
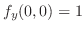 .
.
(b)
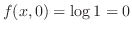 より
より
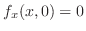 .
したがって,
.
したがって,
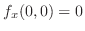 .
.
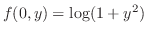 より
より
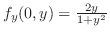 .したがって,
.したがって,
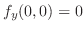 .
.